|
||||||||||
|
|
||||||||||
|
||||||||||
|
|
||||||||||
The velocity typically displayed on these systems is the ground speed, which is defined as the speed at which an object travels relative to a fixed point on the Earth's surface. Mach number, however, is measured with respect to the velocity of the object through the air, or its airspeed. The difference between ground speed and airspeed is caused by the influence of winds on the overall velocity of the aircraft. In past articles, we have discussed differences in flight times between Los Angeles and Bombay as well as London and New York. These discussions explained why flying to the west takes longer than flying to the east and how winds, not the Earth's rotation, cause these differences.
The relationship between ground speed, airspeed, and wind speed can be written in the following form:
If the wind moves in the same direction as the aircraft, the term Vwind will have a positive sign. If the wind blows in the opposite direction as the plane's motion, Vwind will be a negative number.
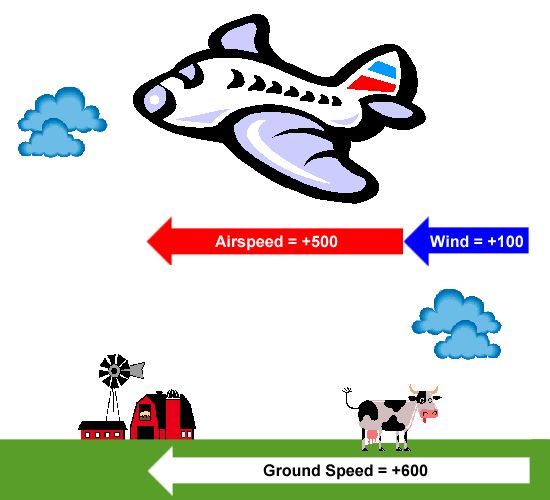
This important distinction between ground speed and airspeed can be better understood by observing the above example. Let's assume that the aircraft's cruise speed, or its speed relative to the local air, is 500 mph. However, the air itself is not motionless but moves at a speed of 100 mph in this example. Let us also assume that the plane is traveling in the same direction as the wind such that it experiences a tailwind of 100 mph. Since the wind and vehicle both move in the same direction, their velocities add together, and the ground speed becomes 600 mph.
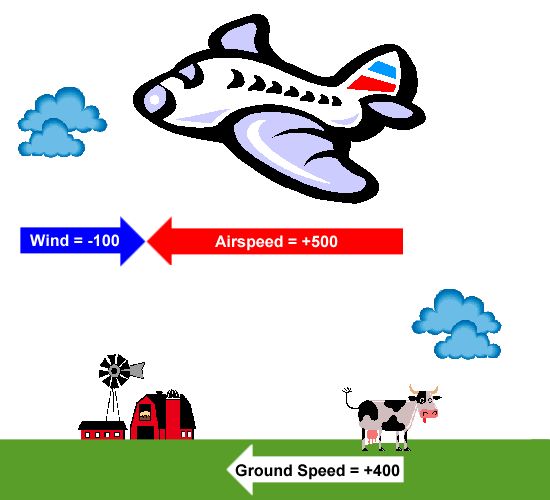
Now let's look at the opposite problem, as illustrated below. In this example, the wind still blows at the same speed with respect to the ground, but its direction is reversed. Now the plane travels against the wind and experiences a headwind of 100 mph. The aircraft is still moving at the same cruise speed of 500 mph with respect to the air, but the difference in the direction of motion of the air means that the wind speed must be subtracted from the plane's airspeed in order to determine the ground speed. The ground speed now becomes only 400 mph.
In these examples, we assumed some round numbers to simplify the explanation. Let us now consider the case described in the question in greater detail. A Boeing 777 has a typical cruise speed of about 560 mph (900 km/h) at an altitude of 35,000 ft (10,675 m). However, the in-flight entertainment system indicated a ground speed of over 700 mph (1,125 km/h). According to the equation shown above, the plane must have encountered a tailwind of at least 140 mph (225 km/h) to make up the difference. While such a wind speed is indeed larger than normal, it is not unheard of at high altitude. Head and tailwinds of around 60 to 80 mph (95 to 130 km/h) are pretty common at these altitudes, and wind speeds approaching 300 mph (480 km/h) are even encountered on occasion in a region known as the jetstream.
Nevertheless, we have pointed out that Mach number is independent of ground speed or wind speed and depends only on the plane's speed relative to the local airflow. Mach number is defined as the ratio of airspeed (V) to the speed of sound (a) at that altitude.
We have previously discussed methods of calculating the speed of sound at a given altitude using the standard atmosphere, and we have also provided tables listing the values of Mach 1 versus altitude. As indicated in the question, the speed of sound at 35,000 ft is 663 mph (1,067 km/h) according to the standard atmosphere model. Even if the plane's ground speed is over 700 mph, however, its airspeed will still be only 560 mph. As a result, the aircraft's Mach number turns out to be about 0.84, or 84% of the speed of sound. In other words, the Boeing 777 never flew faster than the speed of sound during your flight.
It is important to understand this distinction between airspeed and ground speed for other reasons beyond those specifically addressed in this question. The entire field of aerodynamics concerns the forces generated on a body as it moves through some fluid, like air. Most notably, a wing can only create lift if it is moving through the air, or air is moving over it. We can see this dependence most clearly in the lift equation that tells us the lift force depends on the square of the vehicle's speed relative to the air.
Note that I said relative to the air, for the direction the wind is blowing can help or hinder a wing in generating lift. This behavior is particularly important during takeoff and landing. Consider, for example, a typical commercial airliner with a takeoff speed of 180 mph (290 km/h). In other words, the plane would need to accelerate down the runway and achieve a ground speed of 180 mph in order to become airborne on a windless day. Now, consider a wind of 25 mph (40 km/h) blowing along the runway. Let's first assume the wind is a tailwind blowing in the same direction as the aircraft as it moves down the runway. We can now solve for the plane's airspeed using the relationship:
Since the tailwind subtracts from the ground speed of 180 mph, the plane's airspeed is only 155 mph (250 km/h). This speed is insufficient to lift off, so the plane needs a longer runway to make up that extra 25 mph and generate the lift needed to takeoff. Conversely, if that wind is a headwind, it adds to the ground speed. Now the plane can takeoff on a shorter runway since it only needs to accelerate to 155 mph. The extra 25 mph is provided by the wind blowing over the wing to give the plane its needed airspeed of 180 mph.
It is for this reason that an aircraft carrier turns into the wind when planes are being launched. In so doing, the ship creates a headwind over the deck. Carriers normally will speed up as well to create a constant headwind of about 30 knots. The headwind increases the lift on a plane's wings and helps it to takeoff in a shorter distance. Most airport runways are also aligned to take advantage of the prevailing wind directions at that location. Since winds often shift direction over the course of a day, air traffic controllers will redirect planes to different runways at different times to maximize the beneficial effects of headwinds.

Travelers can see many examples of how important the effects of wind are when visiting airports. Devices like the wind sock and anemometer that measure wind direction and speed are located along most runways. These measurement systems provide information that helps controllers best decide how to direct takeoffs and landings to take advantage of the local winds.

The difference between ground speed and airspeed also becomes very important in wind tunnels, like that illustrated above. A wind tunnel works by the principle that the aerodynamic forces on a body are the same whether the object moves through the air or the air moves past the object. The model's position is fixed relative to the tunnel walls, so its ground speed is zero by definition. However, air is blown past the model to create a headwind, and this wind speed gives the model an equal and opposite airspeed.
Additional information about ground speed and airspeed is available at the
NASA Beginner's Guide
to Aerodynamics. This site includes animated examples that illustrate the relationships between airspeed,
ground speed, and wind.
- answer by Jeff Scott, 9 January 2005
Related Topics:
Read More Articles:


|
Aircraft | Design | Ask Us | Shop | Search |

|
|
| About Us | Contact Us | Copyright © 1997-2023 | |||
|
|
|||