|
||||||||||
|
|
||||||||||
|
||||||||||
|
|
||||||||||
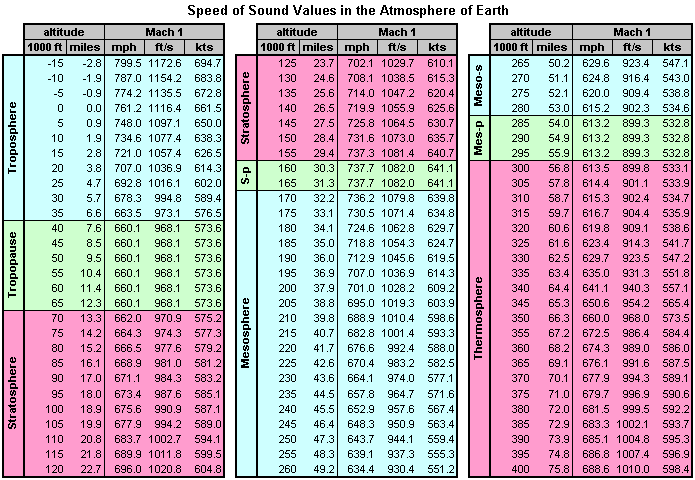
The first table is in the English System and indicates the speed of sound in miles per hour (mph), feet per second (ft/s), and knots (kts) for altitudes from -15,000 ft to 400,000 ft in 5,000 ft increments.
The second table is in the Metric System and indicates the speed of sound in kilometers per hour (km/h), meters per second (m/s), and knots (kts) for altitudes from -4,000 m to 122,000 m in 2,000 m increments.
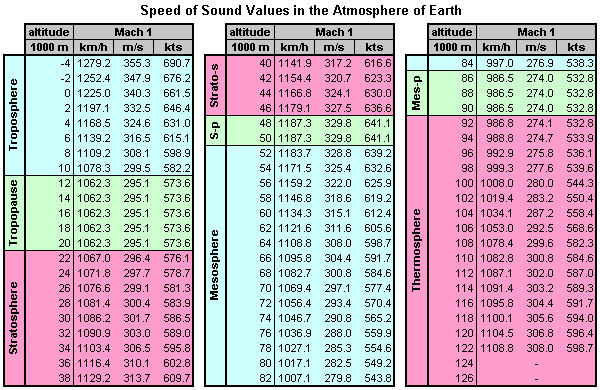
The tables are also color-coded to correspond to different regions of the atmosphere. These regions are defined by the behavior of the atmospheric temperature and (by extension) the speed of sound as altitude increases. These regions include:
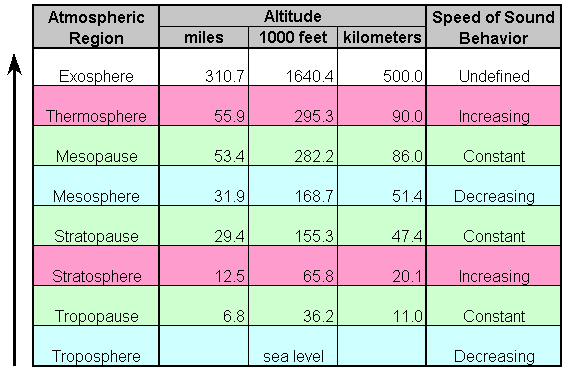
The atmosphere is broken down into regions of decreasing temperature (blue), constant temperature (green), and increasing temperature (red). This behavior is further illustrated below for the Troposphere, Tropopause, Stratosphere, Stratopause, Mesosphere, Mesopause, and lower Thermosphere. Above the Thermosphere is the Exosphere, which is well into what is considered to be space.

The Mach 1 tables are .gif image files that you can download or print for future reference. Furthermore, the tables can be used to determine the speeds associated with multiples of Mach 1. Mach number (M) is a ratio comparing the velocity of a vehicle (V) against the speed of sound (a):
Knowing M and a, we can also rearrange the above equation to the following form to solve for the velocity V:
If you want to know a multiple of the speed of sound at any particular altitude, simply multiply the value of Mach 1 at the altitude of choice by the desired Mach number. For example, Mach 5 at sea level is 5 times the value of Mach 1 at an altitude of 0 ft (0 m):
These tables were created using the 1976 US Standard Atmosphere. Unfortunately, most textbooks and computer programs that provide Standard Atmosphere tables only go up to a height between 200,000 and 295,000 ft (61 to 90 km). Sources that do provide speed of sound values beyond these altitudes are rather contradictory. To extend our tables up to 400,000 ft (122 km), a few known data points were used to linearly interpolate the remaining values. While the Mach 1 values provided for the Thermosphere may not be precise, they should be reasonable approximations. Beyond 400,000 ft (122 km), the air density is so low that the atmosphere essentially ceases to exist and the speed of sound becomes undefined. It is for these reasons that the height of the atmosphere is considered to be about 400,000 ft, or 76 miles (122 km).
You can also verify the results of these tables against our Atmospheric
Properties Calculator. Just enter the altitude and speed to see the corresponding Mach number. Conversely,
the user can also enter the atmosphere and Mach number to see the resulting true airspeed.
- answer by Jeff Scott, 23 February 2003
Related Topics:
How can I calculate the speed of sound on Mars?
Where does the word "Mach" come from? Is it an abbreviation?
Read More Articles:


|
Aircraft | Design | Ask Us | Shop | Search |

|
|
| About Us | Contact Us | Copyright © 1997-2023 | |||
|
|
|||