|
||||||||||
|
|
||||||||||
|
||||||||||
|
|
||||||||||
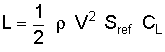
| Variable | Units | Description |
|---|---|---|
| L |
English: lb
Metric: | lift force |
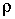
|
English: slugs/ft³
Metric: |
air density Air density changes as a function of altitude, so the value of this variable depends on the height you want to find the lift at. You can find tables of the air properties at different altitudes in the appendices of any elementary aerodynamics book, and you can also compute these properties at the Aerospaceweb.org Atmospheric Properties Calculator. All you need to do is enter the altitude you want and the script will compute the temperature, density, pressure, speed of sound, and other properties at that height. The other input values, like velocity and reference length, are not necessary unless you want to perform the rest of the calculations available. |
| V |
English: ft/s
Metric: |
aircraft velocity The form of velocity applicable to the lift equation is the true airspeed. True airspeed is defined as the actual speed of the aircraft through the air and includes corrections for density, compresibility, and instrumentation error. |
| Sref |
English: ft²
Metric: |
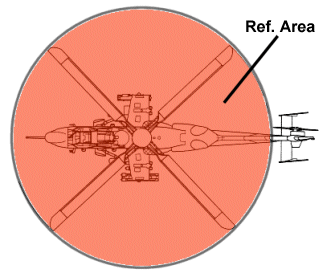
reference area For an airplane, the reference area is the area of the wing when viewed from overhead. This can be somewhat confusing because it includes the area of the wing if it were extended through the fuselage: 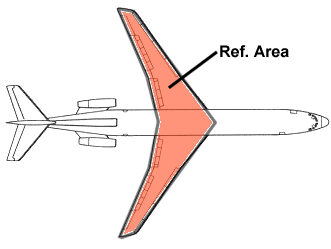
|
| CL | - |
coefficient of lift This variable is a non-dimensional value that changes with speed as well as angle of attack and is dependent on the aircraft. Although CL is usually determined from wind tunnel experiments (or from computational methods that are beyond the scope of this question), the lift coefficient can be estimated fairly accurately for most aircraft. The following graph compares wind tunnel data for two actual aircraft. One set is based on the Cessna 172, a single-engine piston-powered plane that flies at low speeds. The other set of data is for the BAC Lightning, a Mach 2 jet-powered British fighter with a wing sweep of 60°. Planforms of these aircraft are shown along with the lift coefficient graphs.
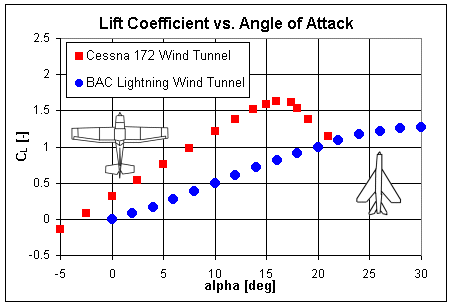
Most aircraft will be behave similarly to the Cessna 172 while high-speed planes with short wingspans, like fighters, will more closely resemble the Lightning data. Unfortunately, I haven't been able to find any comparable results for helicopters. |
Related Topics:
Read More Articles:


|
Aircraft | Design | Ask Us | Shop | Search |

|
|
| About Us | Contact Us | Copyright © 1997-2023 | |||
|
|
|||