|
||||||||||
|
|
||||||||||
|
||||||||||
|
|
||||||||||

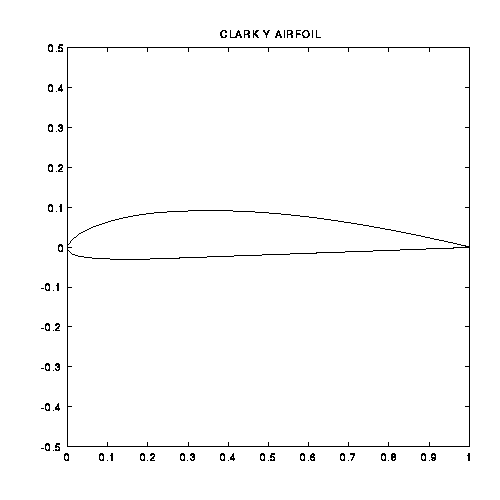
It is this lift force that is produced (primarily) by the wing, and I believe what the questioner means to ask is "How does a wing generate lift?" Though this seems like a simple enough question, the general public would probably be amazed to find out that engineers and scientists still debate just how lift is produced even 100 years after flight became a reality. In fact, it is quite easy to be drawn into charged debates on the subject, as I was when trying to answer this question. So, to be fair to the proponents of each theory, I will discuss each in turn. But first, let us simplify our discussion slightly by thinking of the wing as only a two-dimensional shape. Consider the cross-section of a wing created by a plane cutting through the wing. This two-dimensional cross-sectional shape is called an airfoil (or aerofoil to our British friends). An example of a common airfoil shape is the Clark Y.
Bernoulli theory:
The most common explanation of the concept of lift is based upon the Bernoulli equation, an equation that relates the pressures and velocites acting along the surface of a wing. What this equation says, in simple terms, is that the sum of the pressures acting on a body is a constant. This sum consists of two types of pressures: 1) the static pressure, or the atmospheric pressure at any point in a flowfield, and 2) the dynamic pressure, or the pressure created by the motion of a body through the air. Since dynamic pressure is a function of the velocity of the flow, the Bernoulli equation relates the sum of pressures to the velocity of the flow past the body. So what this equation tells us is that as velocity increases, pressure decreases and vice versa.
To understand why the flow velocity changes, we introduce a second relation called the Continuity equation. What this relationship tells us is that the velocity at which a flow passes through an area is directly related to the size of that area. For example, if you blow through a straw, the air will come out at a certain speed. If you then blow in with the same strength but now squeeze the end of the straw, the air will come out faster.
So how do these equations relate to our two-dimensional airfoil? Look again at the Clark Y and notice that an airfoil is a curved shape. While the bottom is relatively flat, the top surface is thicker and more curved. Thus, when air passes over an airfoil, that flow over the top is squeezed into a smaller area than that airflow passing the lower surface. The Continuity equation tells us that a flow squeezed into a smaller area must go faster, and the Bernoulli equation tells us that when a flow moves faster, it creates a lower pressure. Thus, a higher pressure exists on the lower surface of an airfoil and a lower pressure on the upper surface. Whenever such a pressure difference exists in nature, a force is created in the direction of the lower pressure (since pressure is defined as force per unit area). Think of it as the upper surface being sucked upward. This upward force, of course, is lift. It is this theory that appears in most aerodynamic textbooks, albeit sometimes with incorrect assumptions applied and conclusions drawn.
Newtonian theory:
A theory currently gaining in popularity and arguably more "fundamental" in origin is the Newtonian theory, so named because it is said to follow from Newton's third law of motion (for every action there is an equal and opposite reaction). First, one most realize that any airfoil generating lift deflects the air flow behind it. Positive lift deflects the air downward, towards the ground. Thus, the motion of any lifting surface through a flow accelerates that flow in a new direction. Newton's second law tells us that force is directly proportional to acceleration (F=ma). Therefore, we must conclude from Newton's third law that the force accelerating the air downward must be accompanied by an equal and opposite force pushing the airfoil upward. This upward force is lift.
Circulation theory:
The most mathematical explanation for lift is the circulation theory. Circulation can be thought of as a component of velocity that rotates or swirls around an airfoil or any other shape. In a branch of aerodynamics called incompressible flow, we can use potential flow relationships to solve for this circulation for a desired shape. Once this quantity is known, the force of lift can be solved for using the Kutta-Joukowski theorem that directly relates lift and circulation. This approach tends to be more mathematically intense than I wish to get into here, and it's really more of a method of calculating lift in an ideal flowfield than an explanation of the physical origins of lift.
Conclusion:
So the reader may be asking which of these theories is correct? In truth, each is valid in some respect and useful for certain applications, but the ultimate question is which is the most fundamental explanation. Mathematicians would surely prefer the circulation theory, which is certainly a very elegant approach firmly based on mathematical principles, but it fails to explain what force of nature creates circulation or lift. Many would argue that the Newtonian explanation is most fundamental since it is "derived" from Newtonian laws of motion. While this is true to some degree, the theory lacks an explanation as to why an airfoil deflects the flow downward in the first place. Even accepting this principle, the idea that an airfoil deflects the flow and therefore experiences lift also fails to capture the fundamental tools of nature (pressure and friction) that create and exert that force on the body. Proponents of this explanation generally deride the Bernoulli theory because it relies on less fundamental concepts, like the Bernoulli and Continuity equations. There is some truth to this complaint, and the theory may be more difficult for the novice to understand as a result. However, both equations are derived from Newtonian physics, and I would argue from more fundamental and more mathematically sound premises than the Newtonian theory. In the end, I leave it up to the reader to decide. The following are some sources for further reading on the subject:
Read More Articles:


|
Aircraft | Design | Ask Us | Shop | Search |

|
|
| About Us | Contact Us | Copyright © 1997-2023 | |||
|
|
|||