|
||||||||||
|
|
||||||||||
|
||||||||||
|
|
||||||||||

Before explaining the purpose of dimples, we first need to understand the aerodynamic properties of a sphere. Let us start by looking at a smooth sphere without any dimples, like a ping-pong ball. If we lived in an ideal world without any friction, the air flowing around a smooth sphere would behave like that shown in the following diagram. In this figure, the angle θ represents position along the surface of the sphere. The leading edge of the sphere that first encounters the incoming airflow is at θ=0° while the trailing edge is at θ=180°. A position of θ=90° is the top of the sphere, θ=270° is the bottom, and θ=360° brings us back around to the leading edge. Note that in this ideal situation, the air flowing around the sphere forms a perfectly symmetrical pattern. The streamline pattern around the front face, from 270° up to 90°, is the same as that around the back face, from 90° down to 270°.
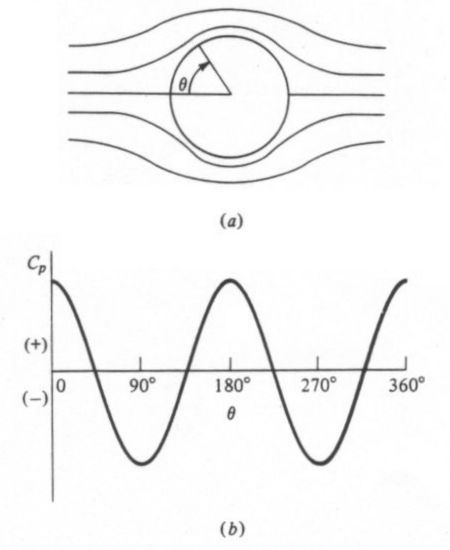
The lower half of this figure also displays the pressure distribution around the surface of the sphere, as represented by the non-dimensional pressure coefficient Cp. Positive (+) values of Cp indicate high pressure while negative (-) values indicate low pressure. It is the differences between high-pressure regions and low-pressure regions that create aerodynamic forces on a body, like lift and drag.
However, this ideal flow pattern tells us something very interesting. Notice that the pressure at the front of the sphere, or θ=0°, is very high. This high pressure indicates that the incoming air impacting against the front face creates a drag force. Nonetheless, the pressure at the back of the sphere, or θ=180°, is also high and identical to that at the front. This high pressure actually creates a thrust, or negative drag, that cancels out the drag on the front of the sphere. In other words, this theoretical situation tells us that there is no drag on a sphere!
Early aerodynamics researchers were quite puzzled by this theoretical result because it contradicted experimental measurements indicating that a sphere does generate drag. The conflict between theory and experiment was one of the great mysteries of the late 19th century that became known as d'Alembert's Paradox, named for famous French mathematician and physicist Jean le Rond d'Alembert (1717-1783) who first discovered the discrepancy.
The reason d'Alembert's ideal theory failed to explain the true aerodynamic behavior of a sphere is that he ignored the influence of friction in his calculations. The actual flowfield around a sphere looks much different than his theory predicts because friction causes a phenomenon known as flow separation. We can better understand this effect by studying the following diagram of the actual flow around a smooth sphere. Here we see that the flowfield around the sphere is no longer symmetrical. Whereas the flow around the ideal sphere continued to follow the surface along the entire rear face, the actual flow no longer does so. When the airflow follows along the surface, we say that the flow is attached. The point at which the flow breaks away from the surface is called the separation point, and the flow downstream of this point is referred to as separated. The region of separated flow is dominated by unsteady, recirculating vortices that create a wake.
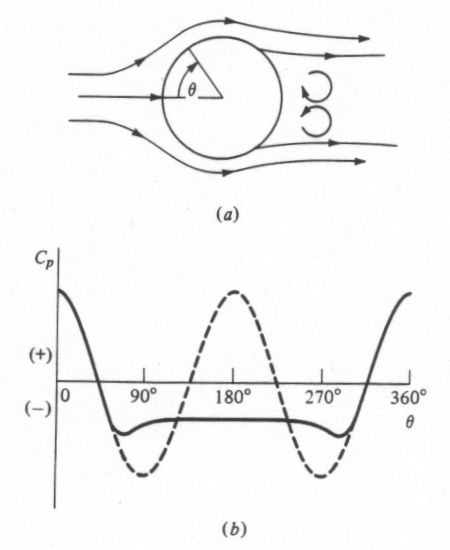
The cause of this separation can be seen in the above pressure distribution around the sphere. As the flow moves downstream from the θ=90° or θ=270° position, it encounters an increasing pressure. Whenever a flow encounters increasing pressure, we say that it experiences an adverse pressure gradient. The change in pressure is called adverse because it causes the airflow to slow down and lose momentum. As the pressure continues to increase, the flow continues to slow down until it reaches a speed of zero. It is at this point that the air no longer has any forward momentum, so it separates from the surface.
Once the flow separates from the surface, it no longer results in the ideal pressure distribution shown as the
dashed line. Instead, a separated flow creates a region of low pressure in the wake. We see this behavior over
the rear face of the sphere from
This explanation leads us to an important conclusion: the drag on a sphere is dominated by the flow separation over its rear face. If we could somehow minimize that separation, the drag experienced by the sphere would be significantly reduced. We can see this effect in experimental data, like that pictured below.
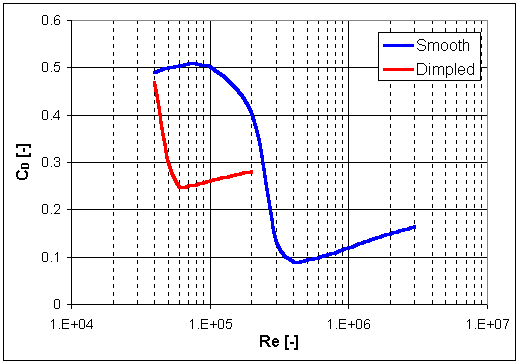
This diagram illustrates how the drag of a sphere varies with the Reynolds number. Reynolds number (Re) is an important non-dimensional parameter that is used to relate the size of an object to the flow conditions it experiences, and is defined by the equation
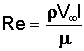
where
What is it about this particular Reynolds number that causes such a large reduction in drag? It turns out that it is at this critical point that the air flowing around the sphere makes an important change. We have already discussed the concept of flow separation. One of the key factors affecting flow separation is the behavior of the boundary layer. The boundary layer is a thin layer of air that lies very close to the surface of a body in motion. It is within this layer that the adverse pressure gradient develops that causes the airflow to separate from the surface.
At low Reynolds numbers, the boundary layer remains very smooth and is called laminar. Laminar boundary layers are normally very desirable because they reduce drag on most shapes. Unfortunately, laminar boundary layers are also very fragile and separate from the surface of a body very easily when they encounter an adverse pressure gradient. This separated flow is what causes the drag to remain so high below the critical Reynolds number.
At that Reynolds number, however, the boundary layer switches from being laminar to turbulent. The location at which this change in the boundary layer occurs is called the transition point. A turbulent boundary layer causes mixing of the air near the surface that normally results in higher drag. However, the advantage of turbulence is that it speeds up the airflow and gives it more forward momentum. As a result, the boundary layer resists the adverse pressure gradient much longer before it separates from the surface.
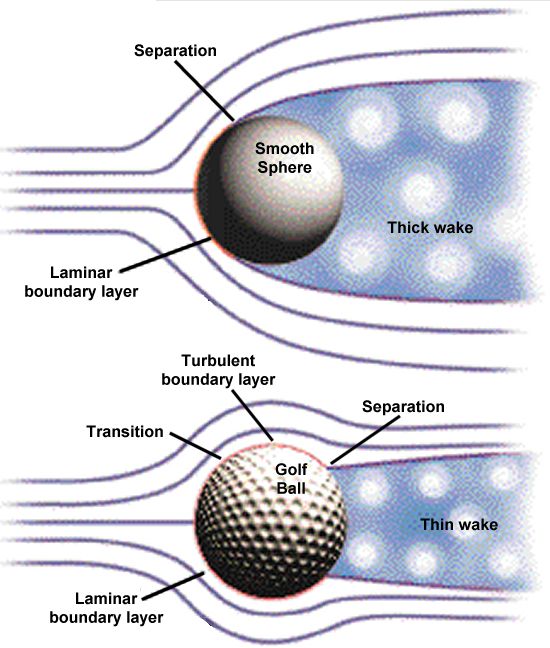
The difference in the flowfields around a smooth sphere and a rough, or dimpled, sphere can be seen above. Since the laminar boundary layer around the smooth sphere separates so rapidly, it creates a very large wake over the entire rear face. This large wake maximizes the region of low pressure and, therefore, results in the maximum difference in pressure between the front and rear faces. As we have seen, this difference creates a large drag like that seen below the transition Reynolds number.
The transition to a turbulent boundary layer, on the other hand, adds energy to the flow allowing it to remain attached to the surface of the sphere further aft. Since separation is delayed, the resulting wake is much narrower. This thin wake reduces the low-pressure region on the rear face and reduces the difference in pressure between the front and back of the sphere. This smaller difference in pressure creates a smaller drag force comparable to that seen above the transition Reynolds number.
These results tell us that causing a turbulent boundary layer to form on the front surface significantly reduces the sphere's drag. For a given sphere diameter, a designer has only two options encourage this transition, either 1) increase the speed of the flow over the sphere to increase the Reynolds number beyond transition or 2) make the surface rough in order to create turbulence. The latter case is often referred to as "tripping" the boundary layer.
In the case of a golf ball, increasing the speed is not an option since a golfer can only swing the club so fast, and this velocity is insufficient to exceed the transition Reynolds number. That leaves tripping the boundary layer as the only realistic alternative to reducing the drag on a golf ball. The purpose of the dimples is to do just that--to create a rough surface that promotes an early transition to a turbulent boundary layer. This turbulence helps the flow remain attached to the surface of the ball and reduces the size of the separated wake so as to reduce the drag it generates in flight. When the drag is reduced, the ball flies farther. Some golf ball manufacturers have even started including dimples with sharp corners rather than circular dimples since research indicates that these polygonal shapes reduce drag even more.

The reason we do not see dimples on other shapes, like wings, is that these particular forms of boundary layer trips only work well on a blunt body like a sphere or a cylinder. The most dominant form of drag on these kinds of shapes is caused by pressure, as we have seen throughout this discussion. More streamlined shapes like the airfoils used on wings are dominated by a different kind of drag called skin friction drag. These streamlined bodies, like that pictured above, have a teardrop shape that creates a much more gradual adverse pressure gradient. This less severe gradient promotes attached flow much further along the body that eliminates flow separation, or at least delays it until very near the trailing edge. The resulting wake is therefore very small and generates very little pressure drag.
However, there do exist other types of devices commonly used on wings that create a similar effect to the dimples used on golf balls. Though these wing devices also create turbulence in order to delay flow separation, the purpose is not to decrease drag but to increase lift. One of the most popular of these devices is the vortex generator.

Vortex generators are often placed along the outer portion of a wing in order to promote a turbulent boundary layer that adds forward momentum to the flow. As in the case of the golf ball, this turbulent boundary layer helps the flow overcome an adverse pressure gradient and remain attached to the surface longer than it would otherwise.

A related device that is most commonly used on high performance fighters is the
leading edge extension (LEX), like that shown above. Both the vortex generator
and the LEX are primarily used to delay the flow separation that occurs when operating at high angles of attack
near stall. As angle of attack increases, the adverse pressure gradient
along the airfoil becomes increasingly stronger. Once the stall angle is reached, the gradient becomes so strong
that it forces the flow to separate resulting in a loss of lift or control effectiveness. The advantage of devices
like vortex generators and leading edge extensions is that they force the flow to remain attached at higher angles
of attack and increase the stall angle. This improvement gives planes likes fighters greater maneuverability
while increasing the safety of commercial airliners.
- answer by Jeff Scott, 13 February 2005
Related Topics:
Read More Articles:


|
Aircraft | Design | Ask Us | Shop | Search |

|
|
| About Us | Contact Us | Copyright © 1997-2023 | |||
|
|
|||