|
||||||||||
|
|
||||||||||
|
||||||||||
|
|
||||||||||
This is particularly true when it comes to collecting wind tunnel data. In the wind tunnel, balances are used to measure the actual lift or drag force as well as aerodynamic moments that are generated by some body in a given set of conditions (such as velocity and angle of attack). Knowing the forces and moments themselves is useful, but it is more convenient to express these values in terms of some nondimesional form that can be more easily compared for different configurations at different conditions.
Let us consider an example and compare the lift produced by a jet fighter to that produced by a sailplane. If you were to compare them simply of the amount of lift force they produce, the fighter would appear to be several orders of magnitude "better" at producing lift. But this is an unfair comparison simply because the fighter weighs orders of magnitude more than the sailplane and needs to generate that much more lift to remain airborne. But when we nondimensionalize the lift force and compare the two vehicles based on their lift coefficients, we'd see that in actuality the sailplane generates a higher lift coefficient making it the more effective lifting surface.
These nondimensional forms of the aerodynamic coefficient are expressed as CL for lift, CD for drag, Cm for pitching moment, and so on. So at this point, what we need is some way to convert the dimensional forces and moments expressed in pounds, Newtons, ounces, foot-pounds, Newton-meters, ounce-inches, or some other unit system into the nondimensional coefficient form. We can understand how this is done by turning back to our good old friend the lift equation:
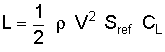
Here we see the dimensional form of lift (L, in pounds or Newtons) is computed as a function of operating conditions (density and velocity), reference area, and the lift coefficient. But in our case, we have specified the operating conditions in the wind tunnel and measured the lift force, so we can compute the lift coefficient in this way:
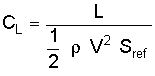
Here it is that we see how the term Sref is needed simply as an area term to nondimensionalize the coefficient. And it really makes no difference what value we use so long as that same value is used consistently in any future work with that coefficient data. It is simply a rule of thumb that the wing area is used as the reference area for aircraft and the rotor area is used for helicopters. For rockets or missiles, we typically use the maximum cross-sectional area of the body. However, this is not always the case as for some missile configurations it makes more sense to use a wing or fin area or even a total planform area. For airfoils, we need a reference length rather than an area, so we use the chord, or length, of the airfoil section.
The key point to remember from this discussion is that the reference area itself has nothing to do with how much lift a vehicle produces, but it is important to know what area was used in a given application to make correct conclusions about the aerodynamic behavior of that body. If one were to conduct two wind tunnel tests of the same missile and in one case used the fin area as the reference area and in the other used the body cross-sectional area, one set of lift coefficients would likely appear to be much greater than the other, so a comparison of the two sets of data would be useless. Therefore, while it is not necessary to use wing area for planes, rotor area for helicopters, or cross-sectional area for missiles, it is useful to do so because it provides a common ground for comparison between the lift coefficient produced by two different planes, two different helicopters, or two different missiles.
As for number of blades and the blade airfoil section, of course these variables factor in to how much lift a
helicopter rotor will generate. But the same can be said of an airplane where the wing airfoil section, the use of
flaps or slats, wing incidence angle, and a variety of other factors will increase or decrease the amount of lift
the plane generates. While these more complex considerations are not addressed directly in the basic equation
for lift, where they do factor in is in the lift coefficient itself. For example, CL increases with
increasing angle of attack for both an aircraft wing and a helicopter rotor. The latter is accomplished by
increasing the angle at which an individual rotor blade or all of the rotor blades collectively meets the oncoming
air. Similarly, the increase in lift associated with a plane dropping flaps or slats is reflected in the lift
equation through an increase in CL. Keep in mind that this equation for lift is only a very basic
expression used to analyze the overall aerodynamic behavior of an entire vehicle. Engineers must use much more
complex methods to do detailed design and analysis work.
- answer by Jeff Scott, 19 May 2002
Related Topics:
Read More Articles:


|
Aircraft | Design | Ask Us | Shop | Search |

|
|
| About Us | Contact Us | Copyright © 1997-2023 | |||
|
|
|||