Mach Number & Similarity Parameters

Mach number is so frequently used to reference speed because it is what we in the aerodynamics world call a similarity parameter. What that term implies is that any vehicle traveling at a given Mach number will experience similar aerodynamic properties, regardless of its altitude or dimensional airspeed. In addition, similarity parameters make it possible to measure the aerodynamic properies of a subscale model in a wind tunnel rather than having to test a full scale vehicle in free flight.

To further investigate the concept, let's take a moment to think about where these similarity parameters come from. In a number of previous questions, we have talked about the lift equation. In those discussions, we have pointed out that lift is dependent upon a number of variables. These same factors also dictate five other aerodynamic forces or moments that act on a vehicle in flight, those being the drag, side-force, pitching moment, yawing moment, and rolling moment. In this example, let us simplify the discussion by focusing on an airfoil cross-section of an airplane's wing. In that case, the aerodynamic quantities of lift, drag, pitching moment generated by the airfoil are dictated by the following variables.

  1. The velocity, or airspeed, at which the plane flies, usually denoted as V∞ (pronounced "V infinity").

  2. The altitude of the aircraft, which defines the density, denoted by the Greek symbol ρ (pronouned "rho").

  3. The size of the lifting surface, or the reference area. For an airplane, we use the wing area denoted by the variable S. Since our airfoil does not have an area, only length, we may substitute a reference length l.

  4. The angle of attack at which the vehicle meets the oncoming airflow, denoted by the Greek symbol α (pronounced "alpha").

  5. The overall shape of the airfoil.

  6. The viscosity of the fluid through which the vehicle flies, which is also a function of the altitude. Viscosity generates friction as the particles of air rush past the airfoil, and this friction induces aerodynamic forces. We represent viscosity by the Greek symbol μ (pronounced "mu").

  7. The compressibility of the airflow. The faster air travels, the more it becomes compressed, or squeezed. It it is compressed enough, shock waves will form causing sudden changes in quantities like density, velocity, and viscosity. Since compressibility is governed by Mach number, we can represent these effects by the variable M∞. But since the Mach number is defined as the velocity divided by the speed of sound and we have already mentioned the importance of velocity, we will simplify to the speed of sound, denoted by the variable a∞.
In other words, for a given airfoil at a given angle of attack, we can say that the lift (L) it generates is a function of velocity, density, reference area or length, viscosity, and speed of sound.

We can write a similar relationship for both the drag (D) and pitching moment (M). If we wanted to use a wind tunnel to measure the variation in L, D, and M for a new airfoil, we could conduct a massive series of tests in which all five of those variables would be changed individually. However, such a series of experiments would take an inordinate amount of time. What if we could combine those variables in such a way that we would only have to vary a couple of parameters in order to fully investigate our airfoil?

When we do so, it can be shown that the lift is proportional to the following quantities:

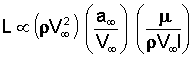
Some of these quantities we have seen before. In particular, the parameter a∞/V∞ is the inverse of the Mach number M∞. The third quantity is also a well known value in the world of aerodynamics called the Reynolds number.

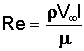
We can therefore simplify our equation to the form

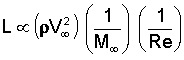
Let us now define a variable called the lift coefficient, which is of the form

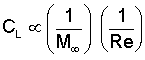
When we plug that definition back into the previous equation, we obtain the following equation for lift, one we have seen many times before.

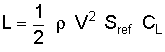
This equation can be simplified even further when we recognize the quantity dynamic pressure:

which leaves us with this deceptively simple equation for lift:

So what has happened here? All of the complex aerodynamics that depend on quantities like viscosity and compressibility effects have been hidden away in the lift coefficient. When we use a wind tunnel to collect aerodynamic data, it is this coefficient we want to measure, because it contains all the dependencies we are concerned about. That's why, in a wind tunnel, we measure the actual lift force L and convert it into a nondimensional coefficient by rearranging the above equation.

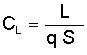
Instead of having to vary the five parameters discussed earlier, we now only need to vary two--Mach number and Reynolds number--and the effects of all other atmospheric properties are automatically included as well. Recall also that the above derivation assumed a constant angle of attack α. We typically must vary this parameter also such that the lift coefficient is a function of three variables.

The true significance of this methodology becomes apparent when we realize that the Mach and Reynolds numbers are both nondimensional numbers. In other words, they are essentially independent of the size of the vehicle. This property allows us to test a small scale version of a real aircraft in a wind tunnel at the same Mach and Reynolds numbers as it would experience in actual flight, and the force and moment coefficients that we measure on this model will be identical to those the real aircraft would experience. When the airflows passing over the real aircraft and a scale model are at the same Mach and Reynolds numbers, we call them dynamically similar flows, which is where the term similarity parameter comes from.

In summation, the reason we so often quote aircraft performance in Mach numbers rather than velocities is because an aircraft traveling at the same Mach number will experience similar aerodynamic behaviors even if all other operating conditions are different. For example, an aircraft flying 685 mph (1,100 km/h) at sea level would be flying subsonically at about Mach 0.9. The same aircraft flying 685 mph at 50,000 ft (15,255 m) would be flying supersonically at about Mach 1.05. A difference of 0.15 Mach may not sound like much, but the behavior of the air flowing around the aircraft changes dramatically as it passes through the speed of sound.
- answer by Joe Yoon, 28 December 2003

Read More Articles:









Back Aircraft | Design | Ask Us | Shop | Search Home
About Us | Contact Us | Copyright © 1997-2023