|
||||||||||
|
|
||||||||||
|
||||||||||
|
|
||||||||||
As you can see, Bernoulli's equation relates the static pressure (p) and velocity (V) of a fluid at point 1 to the pressure and velocity of a fluid at point 2. Static pressure is simply the ambient pressure of the atmosphere resulting from the collisions between all the individual particles making up the atmosphere. The velocity is the speed of the body, such as an airplane or rocket, through the air. Note that the air density, (denoted by the Greek letter rho, ρ) is constant, which means that this equation is only good for incompressible flow. We can usually only assume that air is incompressible at speeds below the speed of sound. This assumption does not hold in the case of space vehicle launches, but that won't matter in a few minutes... Now if we were to examine a flow where the velocity at one point were zero, then we would get a form of Bernoulli's equation that looks like this:
In this equation, p0 is called the total pressure, which is another useful term in aerodynamics. The total pressure is defined as the pressure that would exist if the flow were slowed down isentropically to zero velocity. What does this mean? For an incompressible flow, this equation tells us that the total pressure is constant through the flow! In other words, no matter where you are in the flow, the static pressure plus the term ½ρV² is always the same!
What does this have to do with the Shuttle and "max q"? Nothing necessarily, except that the quantity ½ρV² is important enough that it has been defined as its own quantity called the dynamic pressure, or q.
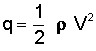
It is easiest to think of this term as the pressure measured due to the physical movement of the air flow as it speeds past a body in motion. For example, think of sticking your hand out of a car window while you are driving down the highway. The faster you go, the more pressure you feel pushing against your hand. The keen observer will note the similarity of q to the definition for kinetic energy (KE):
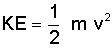
In fact, q is simply the kinetic energy of a unit mass of air.
Okay, back to the Shuttle. Maximum q is usually a factor in all space launches, but we will consider the Shuttle for this example. As the Shuttle ascends during launch, it accelerates quickly. The dynamic pressure q is dependent on the square of the speed, so it must be increasing rapidly as well. Like any vehicle, the structure of the Shuttle can only withstand a certain level of dynamic pressure before it suffers damage. We will call this damaging value of q the "critical q." Before the critical q is reached, the engines of the Shuttle are throttled down to about 65%.
However, while the Shuttle climbs in altitude, not only does the velocity increase rapidly, but the air density decreases rapidly. At some point about one minute after launch and at an altitude of about 35,000 ft (10,675 m), conditions are such that the dynamic pressure has reached "maximum q." After this point, the density begins to drop rapidly enough that the Shuttle can be throttled to full power without fear of structural damage, and the dynamic pressure drops to zero by about 2 minutes after launch.
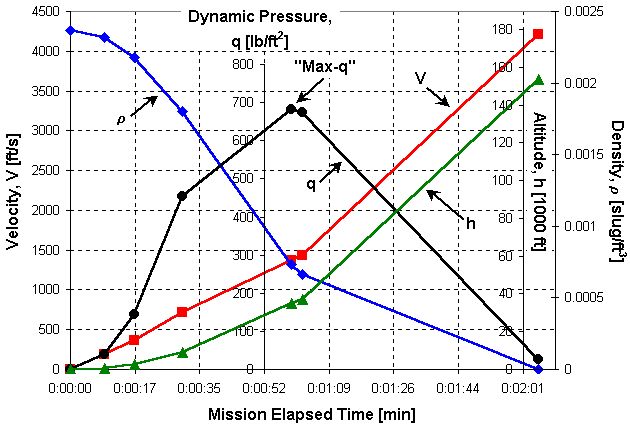
The above figure illustrates how these quantities vary during a typical Shuttle launch. As you can see, the
"maximum q" point occurs about one minute after launch.
- answer by Doug Jackson, 6 May 2001
Related Topics:
Read More Articles:


|
Aircraft | Design | Ask Us | Shop | Search |

|
|
| About Us | Contact Us | Copyright © 1997-2023 | |||
|
|
|||