|
||||||||||
|
|
||||||||||
|
||||||||||
|
|
||||||||||
|
|
|
||||||||||
|
We have already explored various theories used to predict and solve for hypersonic
flowfields. We have also seen the general characteristics of hypersonic vehicles and
various issues the designer must be aware of. We can now learn how waveriders are optimized based on the
characteristics of the assumed flowfield.
Caret Wing:The waverider owes its origins to work done on winged atmospheric reentry vehicles in the 1950s. In 1959, Terence Nonweiler proposed that a three-dimensional hypersonic vehicle could be constructed from a known flowfield, like those described earlier. In particular, Nonweiler chose the flowfield behind a planar oblique shock (the shock formed on a 2D wedge) and used the stream surfaces behind the shock to generate a body shape. Viewed from overhead, the shape looks like a delta wing, but it is actually a concave pyramid shape, known as a caret, as viewed from the aft. The advantage of the caret wing is that the body appears to be riding on top of the attached shock wave at design Mach number, as illustrated below.
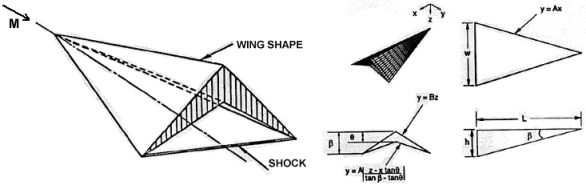
Caret wing showing the attached shock plus a three-view construction [from Corda and Anderson, 1988 and Starkey and Lewis, 1998]Because the planar shock surface is attached at the leading edge, there is no flow spillage from the lower to upper surface. The flow contained beneath the vehicle is at high pressure because of the shock and therefore results in compression lift being generated on the wing’s lower surface. Conical-Flow Waverider:In addition to the simple 2D tangent-wedge flowfield used to design the caret wing, more complicated flowfields can also be used to generate hypersonic bodies. In fact, the flowfield over any axisymmetric body can be used to design a waverider with a shock surface attached along the leading edge. Probably the most commonly used flowfield is that based on conical shapes. Conical shapes typically used include the right circular cone, inclined circular and elliptical cones, yawed circular and elliptical cones, and bodies with longitudinal curvature. Some investigators have gone further using calculus of variations and hypersonic small disturbance theory to search for optimum waverider shapes with high lift-to-drag ratios (see Bowcutt, Anderson and Capriotti, 1987 and Corda and Anderson, 1988). The following figure illustrates in greater detail how conical-flow waveriders are designed. Typically, numerical techniques are used to solve for the inviscid conical shock wave about a cone-shaped surface. The lower surface of the body is defined by the intersection of the conical flow stream surface with the shock wave; this intersection produces the body’s leading edge. The upper surface of the body is usually designed assuming it is a freestream surface or an expansion surface. In the latter case, some small increase in L/D can be gained at the price of a more complicated and time-consuming construction method. The result of this process is a three-dimensional inviscid flow waveriding body, as illustrated below.
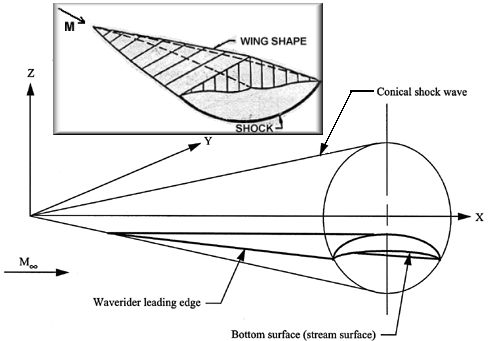
Construction of a body producing a conical shock; (inset) sample conical-flow waverider [from Cockrell, Huebner and Finley, 1995 and Corda and Anderson, 1988]Osculating Cone Waverider:A modification of conical-flow techniques, mentioned previously, is the osculating cones method. Although conical-flow derived waveriders are relatively easy to design, they tend to be prohibitively long and difficult to develop into practical flight vehicles. The advantage of the osculating cones method is that multiple cones are used to design non-axisymmetric shock patterns allowing greater flexibility in vehicle design. For example, a designer can use varying conical shock shapes for different portions of the vehicle to improve performance after the incorporation of engines, crew canopies, control surfaces, and other high-drag items. An example of an osculating cones derived waverider is illustrated below.
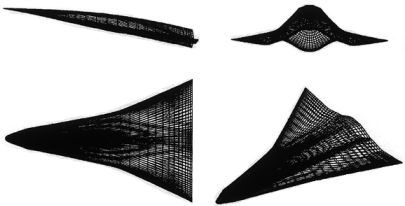
Mach 6 waverider designed using the osculating cones method [from Miller, Argrow, Center, and Brauckmann, 1998]Viscous Waveriders:
The waveriders discussed thus far were all designed assuming inviscid flow (no friction). Since viscous forces
play such a large role in hypersonic flight, we might expect that inclusion of these forces should have a
significant impact on vehicle shape. Starting with conical flow waveriders based on the inviscid analysis
discussed above, researchers have included viscous effects into the design process using integral boundary layer
relationships. The designer need only vary the cone shock angle (
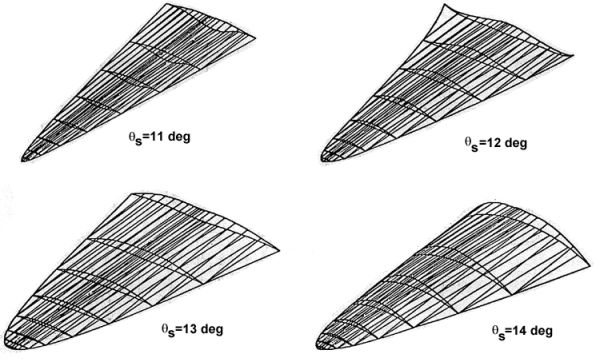
Series of viscous optimized waveriders at Mach 6 [from Bowcutt, Anderson and Capriotti, 1987]In addition, the performance of each vehicle derived for a given design Mach number can be compared to locate a so-called "optimum of the optimums," or the optimum shape for that design Mach number. This is done in the graph below (a), and this plot indicates that the highest L/D value is obtained by the waverider designed for a shock angle of 12°. The resulting vehicle is also shown below (b).
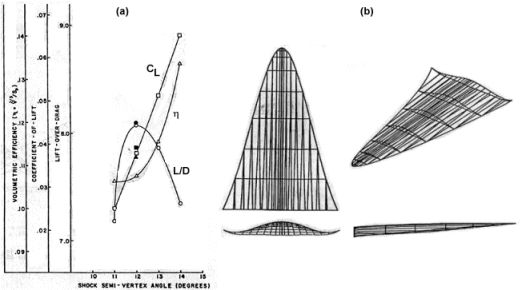
(a) Comparison of waverider performance; (b) optimum Mach 6 waverider (
|


|
Aircraft | Design | Ask Us | Shop | Search |

|
|
| About Us | Contact Us | Copyright © 1997-2023 | |||
|
|
|||