Hypersonic Theory

Introduction History Hypersonic Flow Theory Vehicle Design Waveriders Examples Summary References Home

In the previous section, we alluded to the prediction of aerodynamic properties of hypersonic shapes by taking into account the physical characteristics of hypersonic flow. We will now look more closely at some of the more common theories used to make these predictions. Newtonian Flow Theories: Although he had no knowledge of supersonic or hypersonic flow as such, Isaac Newton was one of the first mathematicians to focus scientific thinking on the fundamental physics of fluid mechanics. In his Principia, published in 1687, Newton proposed that fluid flow consisted of a uniform stream of particles. Should this stream impact on a body, such as the flat plate at an angle of attack a shown below, the normal component of each particle's momentum would be transferred to the plate while the tangential component would be preserved. In this way, the stream of particles would travel along the surface after the collision and be deflected downward, but the particles would have no knowledge of the obstruction until impact. 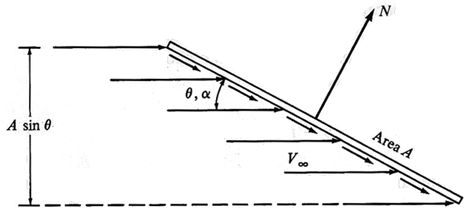Newtonian flowfield over a flat plate [from Anderson, 2000] If Newton had had access to a wind tunnel and some method of flow visualization, he would know that this kind of behavior is incorrect. In actuality, the streamlines passing over a body at subsonic speeds will begin to diverge far upstream of the body, much like water begins to bulge away from the bow of a ship before the ship passes by. However, Newton's analysis is relatively accurate for hypersonic flows because the body moves so quickly that the fluid "cannot see it" before it passes. Because Newton's approach is such a simple one, it is an attractive method for developing simple relationships to predict the aerodynamic properties of bodies at hypersonic speeds. By comparing the rate of change of momentum resulting from the particles impacting the flat plate with the mass flow rate of the particles as they pass by and the change in the force on the plate, we can solve for the coefficient of pressure (C p) on the body: Solving for lift and drag relationships is also quite straightforward yielding the following equations for lift coefficient (C L), drag coefficient (C D), and lift-to-drag ratio (L/D): The aerodynamic predictions derived from Newtonian flow theory are illustrated below. 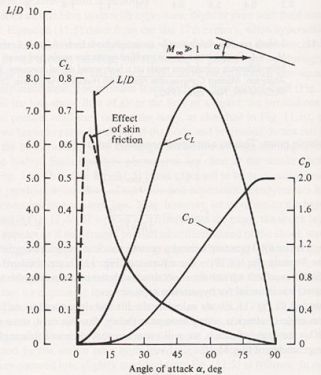Lift and drag predictions derived from Newtonian theory [from Anderson, 2000] From this figure, the following characteristics of hypersonic aerodynamics can be noted: Lift increases with increasing angle of attack, as would be expected, but the maximum lift coefficient occurs at an angle of attack of nearly 55°. This is remarkable since C L max for subsonic bodies typically occurs between 10° and 20°. However, this high angle is realistic for practical hypersonic vehicles. The lift coefficient at low angles of attack (less than 15°) is very nonlinear, in contrast to typical subsonic behavior. The lift-to-drag ratio is maximum at very low angles of attack. Note that L/D would go to infinity as angle of attack goes to 0° if not for the influence of skin friction. In addition to "pure" Newtonian theory, many have proposed corrections and modifications to account for various phenomena ignored in the classical approach. For more information, see pages 53-66 of Anderson, 1989. Although these corrections add greater accuracy for certain hypersonic flow shapes, Newtonian theory is only useful in very elementary applications. Wedge and Conical Flow Methods: Another relatively simple hypersonic flow analysis technique is an approximate method based on equating the body of interest with a two-dimensional wedge. 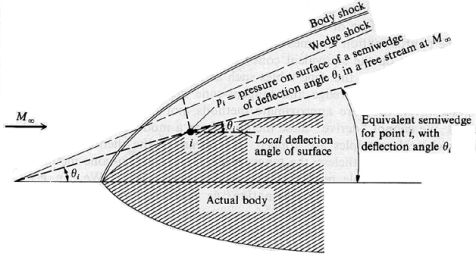The flowfield is determined by constructing a wedge tangent to a given point on the body of interest and assuming that the properties at that point on the wedge are the same as those at the same point on the original body: Tangent-wedge method [from Anderson, 1989] Instead of calculating the flowfield around the body itself, simple oblique shock theory can be applied to the constructed wedge shape to determine the desired properties at the point in question. This technique is known as the wedge or tangent-wedge method. The conical flow, or tangent-cone, method is a similar idea in which the actual body is approximated as a cone-shaped axisymmetric body, as shown below. Thus, the properties at the point under consideration (i) can be obtained from conical flow tables for the correct Mach number. 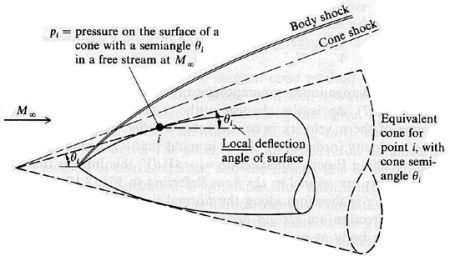Tangent-cone method [from Anderson, 1989] The wedge and cone methods are commonly used in hypersonic analysis methods because they are relatively simple but yield surprisingly accurate results. The conical flow technique is particularly popular and is frequently used to construct hypersonic flowfields from which waveriders are designed. A common variation on the technique is the osculating cones method in which multiple geometrically similar cones are employed. Each cone generates its own shock pattern and the conical shocks are merged together to generate a shock surface of constant strength. Thus, each cone is used to design a small section of the total flowfield. Power Law methods: During the 1960s, it became common practice to describe any hypersonic body of revolution using a parametric equation. The resulting shapes were referred to as power law bodies. Although power law equations can be used to define any shape, such as a wedge or cone, they are usually used to define optimum, minimum drag shapes. 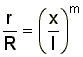Power law bodies are typically defined by an equation of the form where r = radial position, R = body radius, x = axial distance, l = body length, and m is an exponent typically between 0.5 and 0.8. Many references refer to ½ power law bodies (i.e. m = 0.5) or ¾ power law bodies (i.e. m = 0.75), and waveriders have been designed using the known flowfields calculated for such bodies. Other Approaches: The techniques for predicting hypersonic flowfield characteristics discussed above represent only a small fraction of the many methods available. The shock expansion method assumes the flowfield downstream of a two- or three-dimensional body can be determined from Prandtl-Meyer expansion theory. Hypersonic small disturbance theory and thin shock theory are approximate methods used to determine properties in the flowfield between the body and the shock wave. Space-marching finite difference techniques and the method of characteristics are also commonly used to solve for the flowfield over a desired grid space. For more information on these and other hypersonic prediction methods, readers are referred to Anderson, 1989 and Anderson, 1990.

	Aircraft | Design | Ask Us | Shop | Search
	About Us | Contact Us | Copyright © 1997-2023