Hypersonic Flow

Introduction History Hypersonic Flow Theory Vehicle Design Waveriders Examples Summary References Home

Knowing that a waverider is generally intended to travel at hypersonic speeds, we can consider in greater detail the behaviors and properties of hypersonic flows. Thin Shock Layers: Students of aerodynamics know that when a supersonic flow passes over a wedge, a shock wave will form at the point of the wedge. This kind of shock wave is called an oblique shock because it forms at some angle to the surface of wedge (a shock wave perpendicular to the surface is known as a normal shock). As the Mach number increases, the shock angle becomes smaller, as illustrated in the figure below. Therefore, the distance between the wedge surface and the shock decreases with increasing speed. For a hypersonic body, this distance can become very small over a large portion of the body, and the resulting flowfield between the surface and shock is often referred to as a shock layer. This thin layer can produce many complications in vehicle design, e.g. the shock layer may merge with the boundary layer at low Reynolds numbers to form a fully viscous shock layer. 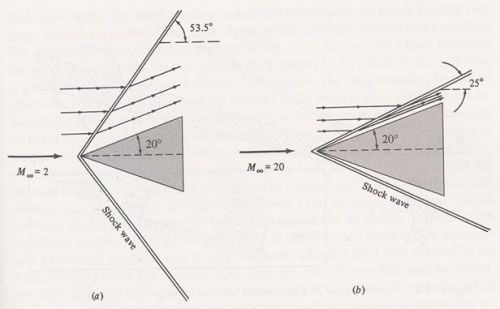Shock waves and streamlines over a 20° half-angle wedge at (a) Mach 2 and (b) Mach 20 [from Anderson, 2000] At high Reynolds numbers, the shock layer can be treated as inviscid (meaning there is no friction). In the limit as Mach number goes to infinity, the shock layer forms an infinitely thin, infinitely dense sheet, or, essentially, a flat plate. The infinite flat plate is the most efficient lifting surface at hypersonic velocities, and the inviscid shock layer can therefore be used to develop simplified theories to predict hypersonic aerodynamic properties. Entropy Layer: The previous discussion related to an oblique shock formed over an ideal wedge with a perfectly sharp leading edge. In practical applications, however, the leading edge must be rounded or blunted in some way both for practicality of manufacture and to ease heat fluxes. Close to this blunt leading edge, the oblique shock becomes highly curved. Shock theory tells us that entropy increases across a shock, and the entropy increase becomes greater as the shock strength increases. Since flow near the nose passes through a nearly normal shock, it will experience a much greater change in entropy compared to flow passing through the much shallower shock angle further from the body centerline. Thus, strong entropy gradients exist near the leading edge generating an "entropy layer" that flows downstream along the body surface. 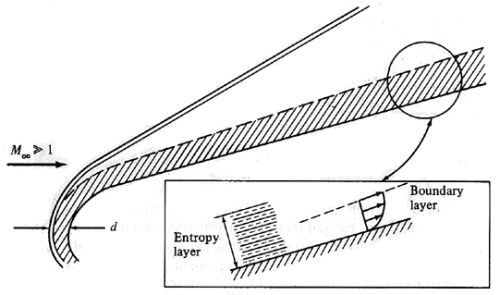Entropy layer formation [from Anderson, 2000] The classical boundary layer grows within this entropy layer and may be greatly affected by the entropy gradients. In addition, the entropy layer is a region of strong vorticity that can generate large gradients in the velocity flowfield near the surface, a phenomenon called "vorticity interaction." The large velocity and thermodynamic gradients induced by the sharply curved oblique shock become troublesome when attempting to predict aerodynamic performance, heat transfer results, and boundary layer shape for a hypersonic vehicle. Viscous Interaction: When a body travels through the air, a thin region near the body surface called the "boundary layer" is formed. In this layer, the air slows down from the "freestream" velocity of the airflow to zero at the surface. 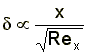At subsonic speeds, the thickness of the boundary layer tends to become smaller as velocity increases because the thickness is inversely proportional to the Reynolds number: For compressible flow (or flow at high speeds), however, increasing flow temperature (due to friction heat) near the body surface causes the boundary layer to become thicker as speed increases. The two primary factors driving this boundary layer growth are an increase in viscosity of the fluid and a decrease in density. 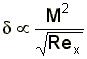The result of these factors is that boundary layer thickness varies as the square of the Mach number: Thus, as Mach number increases, the boundary layer can grow rapidly resulting in very high drag. Should the boundary layer become thick enough, it may affect the inviscid flowfield far from the body, a phenomenon called viscous interaction. Viscous interaction can have a great influence on the surface pressure distribution and skin friction on the body thereby affecting the lift, drag, stability, and heating characteristics of the body. High Temperature Flow: As previously mentioned, travel at high velocities produces friction and heat. Part of the kinetic energy of the body's motion is absorbed by the air and carried away from the body through a process called viscous dissipation. However, hypersonic vehicles create so much heat and such high temperatures that they can actually cause chemical changes to occur in the fluid through which they fly. The most notable changes air undergoes as temperature increases are summarized below. High Temperature Effects on Air Temperature [K] Chemical Change 800 Molecular vibration 2000 Oxygen molecules (O 2) dissociate 4000 Nitrogen molecules (N 2) dissociate Nitric oxide (NO) forms 9000 Oxygen and nitrogen atoms ionize As temperature increases, assumptions about the properties of the air are no longer valid and the vehicle is said to be traveling through a chemically reacting boundary layer. When the properties of the working fluid change, namely density and heat transfer properties, the aerodynamic characteristics and heating properties of the body can change drastically. Low Density Flow: Although the properties of low density flow are not necessarily applicable to hypersonic flight, most hypersonic vehicles are intended to cruise at high altitudes in low density fluids. Therefore, these flow conditions are often important in waverider design. In low density flows, air can no longer be considered to be a continuum because the distance between individual particles of air becomes so great that each particle begins to affect the aerodynamic properties of a body. Under these conditions, common aerodynamic relations, like the Euler and Navier-Stokes equations, break down. Instead, aerodynamic properties must be analyzed using kinetic theory. Some of the most important differences between low density flows and continuous flows include Velocity slip: The viscous no-slip condition that says the velocity of air particles going past a body must be zero at the body surface, fails. Since friction is negligible in low density, the flow velocity at the body surface is no longer zero. Temperature slip: The assumption that gas temperature at the body surface becomes equal to the temperature of the body surface material fails. Most equations derived from the continuum assumption can still be used once these slip conditions begin to take effect so long as correcting terms are added. Eventually, however, density becomes so small that fluid particles interact only with the vehicle itself and do not impact each other. In this free-molecule flow, flow structure becomes poorly defined and shocks are thick and indistinct. The aerodynamic and thermodynamic properties of the vehicle are affected at the molecular level. For example, the following figure indicates how greatly the drag coefficient of a sphere can vary when transitioning from a continuum flow to a free-molecule flow (where Kn is the Knudson number, a nondimensional parameter related to the distance between molecules). 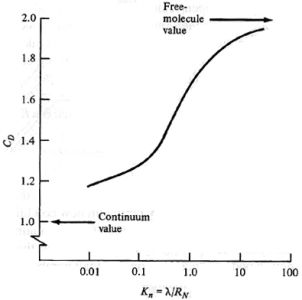Drag coefficient of a sphere at hypersonic speeds transitioning from continuum to free-molecule flow [from Anderson, 2000] Combined Effect: Described above are the most important flow properties resulting from travel at hypersonic velocities. Each factor plays a large role in the design and operation of a practical hypersonic vehicle, as will be seen in following sections. The principal characteristics of hypersonic flow are summarized in the following figure. 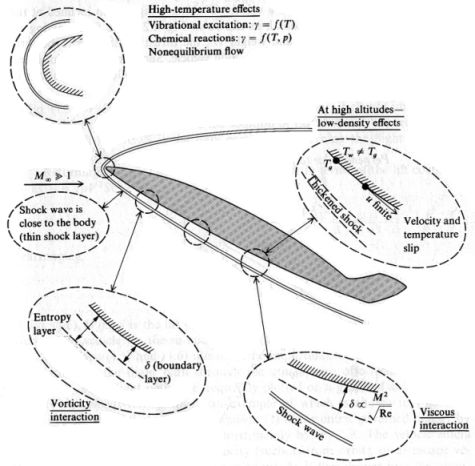Characteristics of hypersonic flow [from Anderson, 1989]

	Aircraft | Design | Ask Us | Shop | Search
	About Us | Contact Us | Copyright © 1997-2023