|
||||||||||
|
|
||||||||||
|
||||||||||
|
|
||||||||||
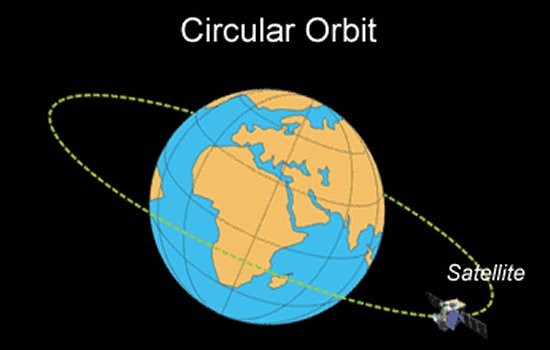
That disclaimer aside, let us begin our discussion by defining some terminology. The word "orbit" is defined as the path a body follows when being acted upon by the force of gravity. We typically think of an orbit as the path a heavenly body or space vehicle follows as it revolves around another body, which we will call the primary body. For example, a communications satellite follows an orbital path around the Earth and the Earth follows an orbital path around the Sun. The study of artificial satellites and space vehicles moving under the influence of forces like gravity (as well as drag and thrust) is called "orbital mechanics."
The one equation that is at the heart of orbital mechanics is Newton's second law of motion. This law tells us that applying a force (F) to an object with mass (m) causes it to accelerate (a). We will use this equation again momentarily.
Another key equation that Newton handed down to us is his law of universal gravitation. In this relationship, Newton describes the mutual attraction between two objects with mass. Simply put, the law of universal gravitation says that two objects having mass M and m and separated by a distance r are attracted to each other with equal and opposite forces directed along the line joining the objects. The magnitude of that force (F) is given by:
This equation introduces a new variable called G, or the universal constant of gravitation. This constant describes the mutual attraction between two separate masses, and is equal to:
Substituting this equation for acceleration into Newton's second law gives us the following equation for uniform circular motion:
If we set this equation equal to the Newton's law of universal gravitation, we can solve for the circular velocity (v).
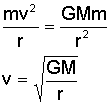
Note how simple this equation is. It says that the velocity of an object in a circular orbit is proportional to nothing more than the mass of the primary body and the radius of the circular orbit. In our example, the primary body is the Earth and the orbiting body is the Space Shuttle, so we can use this equation to solve for the Shuttle's orbital speed.
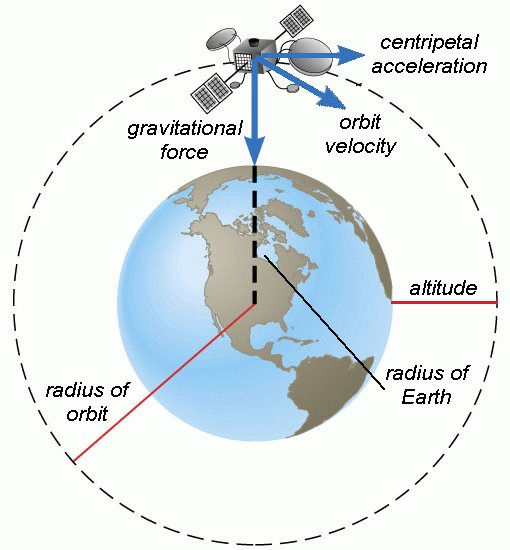
To make the solution a bit more obvious, let us specify the mass M as the mass of Earth (ME) and break the radius of orbit into the radius of Earth (RE) plus the altitude of the Shuttle above the Earth's surface (h).
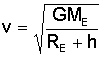
where
RE = 6.375 x 106 m in the Metric system
RE = 2.091 x 107 ft in the English system
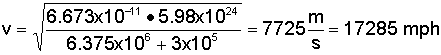
This speed is about what we should expect since the Shuttle typically orbits the Earth at about 17,500 mph (28,165 km/h). However, it should be noted that the Shuttle's orbit, in reality, is usually not a perfect circle. The orbit is typically slightly elliptical, or elongated, and looks more like an oval than a true circle. The equations we have discussed here are nevertheless a pretty close approximation of the Shuttle orbit.
In addition, these same relationships can be used to describe other bodies in orbit as well. For example, a special class of orbit is called the geostationary or geosynchronous orbit, often abbreviated as GEO. A satellite in geostationary orbit takes exactly 24 hours to orbit the Earth such that the satellite appears to remain stationary above the same point on the Earth at all times. This type of orbit is ideal for many communications and weather satellites. A geostationary orbit has an altitude of 22,240 miles (35,790 km), which results in an orbital speed of 6,880 mph (11,070 km/h).
We can also apply the same equation to the orbit of the Earth around the Sun. This orbit is also not a perfect circle, but is pretty close to get a good estimate of the Earth's orbital speed. In this case, the value of M becomes the mass of the Sun (MS) and the radius of orbit is the average distance from the Sun to Earth (REarth orbit).
Related Topics:
Read More Articles:


|
Aircraft | Design | Ask Us | Shop | Search |

|
|
| About Us | Contact Us | Copyright © 1997-2023 | |||
|
|
|||