Aerospaceweb.org | Ask Us - Gravity on Other Planets

Gravity on Other Planets

- question from Kashim Grema

The universal constant of gravitation (G) is an important variable frequently used in fields like orbital mechanics where it plays a role in calculating parameters such as orbital speed. Acceleration due to gravity (g) is also an important variable used to calculate properties like speed near the surface of a planet or other large body.

The value of G is a constant that should not change no matter where one is in the universe. The value of g, however, does vary for each planet, star, moon, or other large body based on its size and mass. These two gravitational parameters are related by the equation:

where

The value of G is known and has been estimated by scientists as:

^-11

^-8

Using this relationship, we can solve for the acceleration due to gravity on any planet so long as we know the planet's size. The acceleration due to gravity of Earth, for example, is known to be about 9.81 m/s² or 32.2 ft/s². Let us verify this value by plugging the Earth's mass (M_E) and radius (R_E) into the above equation.

²⁴

²³

R_E = 6.375 x 10⁶ m in the Metric system
R_E = 2.091 x 10⁷ ft in the English system

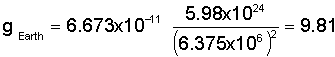
When we do so, we find that the Earth's acceleration due to gravity is indeed about 9.81 m/s².

Scale drawing of the relative sizes of planets and moons in the solar system

We can go even further by using this relationship to solve for the acceleration due to gravity on other planets or moons. The following table provides the mass, radius, and gravitational acceleration of several major bodies within our solar system.

Acceleration Due to Gravity Comparison
Body	Mass [kg]	Radius [m]	Acceleration Due to Gravity, "g" [m/s²]	g / g-Earth
Sun	1.99 x 10³⁰	6.96 x 10⁸	274.13	27.95
Mercury	3.18 x 10²³	2.43 x 10⁶	3.59	0.37
Venus	4.88 x 10²⁴	6.06 x 10⁶	8.87	0.90
Earth	5.98 x 10²⁴	6.38 x 10⁶	9.81	1.00
Moon	7.36 x 10²²	1.74 x 10⁶	1.62	0.17
Mars	6.42 x 10²³	3.37 x 10⁶	3.77	0.38
Jupiter	1.90 x 10²⁷	6.99 x 10⁷	25.95	2.65
Saturn	5.68 x 10²⁶	5.85 x 10⁷	11.08	1.13
Uranus	8.68 x 10²⁵	2.33 x 10⁷	10.67	1.09
Neptune	1.03 x 10²⁶	2.21 x 10⁷	14.07	1.43
Pluto	1.40 x 10²²	1.50 x 10⁶	0.42	0.04

The last column of the table compares the acceleration due to gravity of the body to that of Earth. A small body like the Moon only exerts a gravitational acceleration about 1/6th as strong as that of Earth while the massive Sun generates an acceleration nearly 28 times that of Earth. Tiny Pluto, meanwhile, only exerts about 4% the gravity of Earth.

This information is also useful since it directly corresponds to how much an object would weigh on the surface of each of these bodies. We have previously discussed the relationship between weight, mass, and gravity in a number of articles. As we have seen, the mass of an object remains constant whether it is on the surface of Earth, the surface of the Moon, or in the depths of space. The quantity that does change depending on the strength of the gravitational field is the object's weight. These variables are related by the equation:

where

Since we now know the acceleration due to gravity on different worlds, we can easily determine how much an object weighs on those bodies. We have shown that the value of "g" on the Moon is 1/6th that of Earth, so an object on the Moon weighs only 1/6th as much as it would on Earth. A person weighing 150 pounds on Earth, for example, would weigh only 25 pounds on the Moon.

Another place in the solar system humans are likely to visit in the future is Mars. Although Mars is the planet most like Earth in terms of its environment, the gravitational acceleration on this much smaller planet is only about 40% that of Earth. Mars is also farther from the Sun and takes longer to complete an orbit, so a Martian year is about twice as long as a year on Earth. On this Mother's Day, you might consider offering the women in your life a trip to the distant red planet. After all, what woman wouldn't like the idea of having her weight and age cut in half?!
- answer by Joe Yoon, 8 May 2005

Aircraft | Design | Ask Us | Shop | Search