|
||||||||||
|
|
||||||||||
|
||||||||||
|
|
||||||||||
However, your understanding of the definition of acceleration is not correct. An object falling under the force of gravity will always experience the same acceleration of 32 ft/s² as time increases. What does change over time is the velocity of the object. Since the acceleration due to gravity is a constant value that does not change, we can apply a series of relationships called the uniform acceleration formulas. Acceleration (a) is defined as the change in velocity (v) over time (t):
In our case, we know the acceleration and want to solve for the velocity, so we can rearrange that equation into the following form:
Furthermore, we can also calculate the distance (d) traveled over time under the influence of a uniform acceleration by the equation:
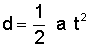
The above equation for velocity can be used to solve the specific question you ask about. We have established that the acceleration in this case is a constant of 32 ft/s². By using that value for the variable "a" and letting "t" equal 1 second, 2 seconds, and so on, we find that an object falling to the Earth's surface will be traveling at a velocity of 32 ft/s at the end of the first second, 64 ft/s the second, 96 ft/s the third, and so on. We can solve for the distance traveled in a similar manner to find that the object falls 16 ft at the end of the first second, 64 ft the second, 144 ft the third, etc. These results are summarized in the following table.
Time | Acceleration | Velocity | Distance [sec] | [ft/s²] [m/s²] | [ft/s] [m/s] | [ft] [m] ======|=================|===============|============ 0 | 32 10 | 0 0 | 0 0 1 | 32 10 | 32 10 | 16 5 2 | 32 10 | 64 20 | 64 20 3 | 32 10 | 96 30 | 144 45 4 | 32 10 | 128 40 | 256 80 5 | 32 10 | 160 50 | 400 125 6 | 32 10 | 192 60 | 576 180 7 | 32 10 | 224 70 | 784 245 8 | 32 10 | 256 80 | 1024 320 9 | 32 10 | 288 90 | 1296 405 10 | 32 10 | 320 100 | 1600 500 |
Time | Acceleration | Velocity | Distance [sec] | [ft/s²] [m/s²] | [ft/s] [m/s] | [ft] [m] ======|===================|==================|================ 0.0 | -32.17 -9.81 | 0.00 0.00 | 1211.00 369.00 0.5 | -32.17 -9.81 | -16.09 -4.91 | 1206.98 367.77 1.0 | -32.17 -9.81 | -32.17 -9.81 | 1194.92 364.10 1.5 | -32.17 -9.81 | -48.26 -14.72 | 1174.81 357.96 2.0 | -32.17 -9.81 | -64.34 -19.62 | 1146.66 349.38 2.5 | -32.17 -9.81 | -80.43 -24.53 | 1110.47 338.34 3.0 | -32.17 -9.81 | -96.51 -29.43 | 1066.24 324.86 3.5 | -32.17 -9.81 | -112.60 -34.34 | 1013.96 308.91 4.0 | -32.17 -9.81 | -128.68 -39.24 | 953.64 290.52 4.5 | -32.17 -9.81 | -144.77 -44.15 | 885.28 269.67 5.0 | -32.17 -9.81 | -160.85 -49.05 | 808.88 246.38 5.5 | -32.17 -9.81 | -176.94 -53.96 | 724.43 220.62 6.0 | -32.17 -9.81 | -193.02 -58.86 | 631.94 192.42 6.5 | -32.17 -9.81 | -209.11 -63.77 | 531.41 161.76 7.0 | -32.17 -9.81 | -225.19 -68.67 | 422.84 128.66 7.5 | -32.17 -9.81 | -241.28 -73.58 | 306.22 93.09 8.0 | -32.17 -9.81 | -257.36 -78.48 | 181.56 55.08 8.5 | -32.17 -9.81 | -273.45 -83.39 | 48.86 14.61 9.0 | -32.17 -9.81 | -289.53 -88.29 | -91.89 -28.31 |
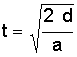
Simply use the height of the building and the acceleration due to gravity to calculate that it takes about 8.68 seconds for the penny to reach the ground. We can then return to the equation that tells us velocity is the product of acceleration and time to solve for the penny's speed once it hits the ground. This velocity turns out to be 279 ft/s (85 m/s), or about 190 mph (305 km/h)!
However, you need not fear walking next to tall buildings because a penny will actually never be able to fall that fast. Why? Our simple analysis has neglected one very important fact--the Earth has an atmosphere. Why should this factor matter? Notice that nowhere in any of the equations we have used so far does the size or weight of the falling object appear. We could have dropped an automobile from the top of the Empire State Building, and the uniform acceleration equations tell us that it would reach the ground in the same amount of time at the same speed as our penny.
However, we know intuitively that this cannot be true. Imagine holding up a sheet of paper and a book and dropping them to the floor. Would they land at the same time? Our experiences tell us that the heavy book will hit the floor much faster while the light piece of paper will slowly float to a gentle landing. The difference between our real-life experiences and these ideal equations is that the equations do not take into account the influence of the air in which we live. The Earth's atmosphere creates a force called drag, or a resistance to motion that slows a falling object down and reduces its acceleration. We can see this resistance even more clearly in thicker, denser fluids. For example, imagine dropping a heavy metal ball bearing into water or a can of paint, and it takes much longer to settle to the bottom because of the resistance of the fluid.
Because of the resistance created by drag, an object in free-fall will not behave as though it is influenced by a uniform acceleration. The object's acceleration will instead continually decrease until it reaches zero and the velocity becomes a constant. We call this final speed of a falling object its terminal velocity, a speed that will vary from object to object. In the example described above, a heavy book has a much higher terminal velocity than a light sheet of paper, which is why the book hits the floor first.
The process of calculating terminal velocity is more complex and requires us to know something about an object's aerodynamic characteristics, particularly its drag. We have seen in previous articles that the drag force can be calculated using the equation:
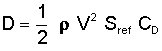
where
Terminal velocity is achieved once the drag that is pushing against the falling object's motion becomes equal to the weight of the object pulling it downward. We have seen in previous articles that weight is calculated by the following relationship:
where
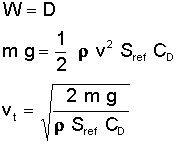
Let's again return to our example of the falling penny. An American penny minted today has a mass of 2.5 grams, or 0.00017 slug (0.0025 kg). The drag coefficient of a circular disk, like a penny, has been measured as 1.17 assuming the reference area is the frontal area of the disk. A penny has a diameter of about ¾ inch (19 mm), so the area of one of its faces will be approximately 0.00305 ft² (0.00028 m²). Note that the penny is likely to tumble so that its face is not always perfectly aligned with the flow, causing the drag coefficient to vary. This tumbling behavior is an unsteady motion that is difficult to predict, so we will assume the drag is a constant in our example. The atmospheric density changes with altitude, but it changes by less than 1% for the relatively short distance we are concerned about here. As a result, we will treat the density as a constant and use the standard sea level value of 0.0023769 slug/ft³ (1.225 kg/m³). We can now use these values in the above relationship to solve for the terminal velocity.
When we do so, we find that the maximum speed the penny can reach is only 36 ft/s (11 m/s), or 25 mph (40 km/h). This speed is 87% lower than that predicted using the uniform acceleration equations described earlier. The following table illustrates the motion of the penny over time. Note how much longer it takes for the penny to reach the ground when compared to the constant acceleration table presented above.
Time | Weight | Drag | Acceleration | Velocity | Distance [sec] | [lb] [N] | [lb] [N] | [ft/s²] [m/s²] | [ft/s] [m/s] | [ft] [m] ======|==================|================|==================|=================|================ 0.00 | -0.0055 -0.0245 | 0.0000 0.0000 | -32.17 -9.81 | 0.00 0.00 | 1211.00 369.00 1.00 | -0.0055 -0.0245 | 0.0028 0.0126 | -16.08 -4.91 | -25.78 -7.87 | 1194.88 364.54 2.00 | -0.0055 -0.0245 | 0.0049 0.0220 | -3.41 -1.04 | -34.12 -10.41 | 1163.82 355.06 3.00 | -0.0055 -0.0245 | 0.0054 0.0241 | -0.58 -0.18 | -35.70 -10.89 | 1128.67 344.34 4.00 | -0.0055 -0.0245 | 0.0055 0.0245 | -0.09 -0.03 | -35.96 -10.97 | 1092.80 333.40 5.00 | -0.0055 -0.0245 | 0.0055 0.0245 | -0.02 0.00 | -36.00 -10.98 | 1056.81 322.42 6.00 | -0.0055 -0.0245 | 0.0055 0.0245 | 0.00 0.00 | -36.01 -10.99 | 1020.81 311.43 7.00 | -0.0055 -0.0245 | 0.0055 0.0245 | 0.00 0.00 | -36.01 -10.99 | 984.80 300.45 8.00 | -0.0055 -0.0245 | 0.0055 0.0245 | 0.00 0.00 | -36.01 -10.99 | 948.78 289.46 9.00 | -0.0055 -0.0245 | 0.0055 0.0245 | 0.00 0.00 | -36.01 -10.99 | 912.77 278.47 10.00 | -0.0055 -0.0245 | 0.0055 0.0245 | 0.00 0.00 | -36.01 -10.99 | 876.76 267.49 11.00 | -0.0055 -0.0245 | 0.0055 0.0245 | 0.00 0.00 | -36.01 -10.99 | 840.75 256.50 12.00 | -0.0055 -0.0245 | 0.0055 0.0245 | 0.00 0.00 | -36.01 -10.99 | 804.74 245.51 13.00 | -0.0055 -0.0245 | 0.0055 0.0245 | 0.00 0.00 | -36.01 -10.99 | 768.73 234.53 14.00 | -0.0055 -0.0245 | 0.0055 0.0245 | 0.00 0.00 | -36.01 -10.99 | 732.72 223.54 15.00 | -0.0055 -0.0245 | 0.0055 0.0245 | 0.00 0.00 | -36.01 -10.99 | 696.70 212.55 16.00 | -0.0055 -0.0245 | 0.0055 0.0245 | 0.00 0.00 | -36.01 -10.99 | 660.69 201.57 17.00 | -0.0055 -0.0245 | 0.0055 0.0245 | 0.00 0.00 | -36.01 -10.99 | 624.68 190.58 18.00 | -0.0055 -0.0245 | 0.0055 0.0245 | 0.00 0.00 | -36.01 -10.99 | 588.67 179.59 19.00 | -0.0055 -0.0245 | 0.0055 0.0245 | 0.00 0.00 | -36.01 -10.99 | 552.66 168.61 20.00 | -0.0055 -0.0245 | 0.0055 0.0245 | 0.00 0.00 | -36.01 -10.99 | 516.65 157.62 21.00 | -0.0055 -0.0245 | 0.0055 0.0245 | 0.00 0.00 | -36.01 -10.99 | 480.64 146.63 22.00 | -0.0055 -0.0245 | 0.0055 0.0245 | 0.00 0.00 | -36.01 -10.99 | 444.62 135.65 23.00 | -0.0055 -0.0245 | 0.0055 0.0245 | 0.00 0.00 | -36.01 -10.99 | 408.61 124.66 24.00 | -0.0055 -0.0245 | 0.0055 0.0245 | 0.00 0.00 | -36.01 -10.99 | 372.60 113.68 25.00 | -0.0055 -0.0245 | 0.0055 0.0245 | 0.00 0.00 | -36.01 -10.99 | 336.59 102.69 26.00 | -0.0055 -0.0245 | 0.0055 0.0245 | 0.00 0.00 | -36.01 -10.99 | 300.58 91.70 27.00 | -0.0055 -0.0245 | 0.0055 0.0245 | 0.00 0.00 | -36.01 -10.99 | 264.57 80.72 28.00 | -0.0055 -0.0245 | 0.0055 0.0245 | 0.00 0.00 | -36.01 -10.99 | 228.56 69.73 29.00 | -0.0055 -0.0245 | 0.0055 0.0245 | 0.00 0.00 | -36.01 -10.99 | 192.55 58.74 30.00 | -0.0055 -0.0245 | 0.0055 0.0245 | 0.00 0.00 | -36.01 -10.99 | 156.53 47.76 31.00 | -0.0055 -0.0245 | 0.0055 0.0245 | 0.00 0.00 | -36.01 -10.99 | 120.52 36.77 32.00 | -0.0055 -0.0245 | 0.0055 0.0245 | 0.00 0.00 | -36.01 -10.99 | 84.51 25.78 33.00 | -0.0055 -0.0245 | 0.0055 0.0245 | 0.00 0.00 | -36.01 -10.99 | 48.50 14.80 34.00 | -0.0055 -0.0245 | 0.0055 0.0245 | 0.00 0.00 | -36.01 -10.99 | 12.49 3.81 34.34 | -0.0055 -0.0245 | 0.0055 0.0245 | 0.00 0.00 | -36.01 -10.99 | 0.24 0.07 34.36 | -0.0055 -0.0245 | 0.0055 0.0245 | 0.00 0.00 | -36.01 -10.99 | -0.48 -0.15 |
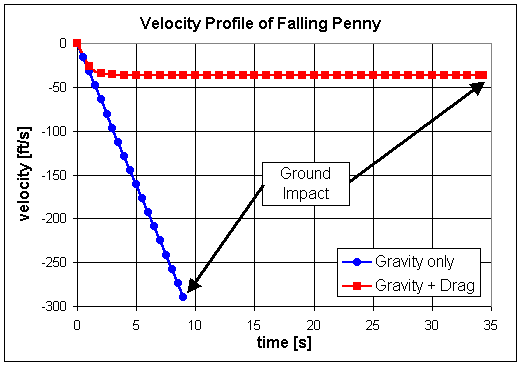
Our two approaches have told us that a penny dropped from the top of the Empire State Building could reach anywhere from 25 to 190 mph (40 to 305 km/h) by the time it hits the ground. We have shown that the higher value is unrealistic because it ignores air resistance, but even the lower value may sound too high for the comfort of some readers. However, we must remember that a penny has a very low mass, and the energy the penny has when it hits the ground will also be quite low. We can calculate the kinetic energy (KE) of the penny by the following equation:
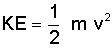
This relationship tells us that the penny generates a maximum energy of about 6.6 ft-lb (9 Joules) assuming uniform acceleration, but only 0.11 ft-lb (0.15 J) at its terminal velocity. For comparison, a typical BB or pellet fired by a low-powered air gun produces about 4 to 15 ft-lb (5 to 20 J) of energy. This energy may be sufficient to break the skin but usually does no worse than create a brief stinging sensation. Compare these miniscule energies to a standard pistol with a muzzle energy of 300 ft-lb (400 J) or a high-powered rifle that generates an energy of 3,000 ft-lb (4,000 J). Even assuming the worst case, a penny has too little energy to do any harm to a person. A realistic penny drop that includes the effects of drag will barely be noticeable.
Even though the uniform acceleration equations have their limitations, we shouldn't discard them for they can still tell us much about the physics of motion. These equations are particularly useful in understanding the motion of objects through the vacuum of space, where there is no atmosphere to produce drag. The accuracy of these relationships was perhaps best illustrated by NASA astronaut David Scott who journeyed to the Moon aboard Apollo 15.

One of the experiments Scott conducted was to drop a feather and a hammer on the Moon's surface, where there is no
atmosphere. His test confirmed that these two objects of very different mass would indeed hit the ground at the
same time when acted upon only by the acceleration due to gravity. The results of Scott's experiment can be
observed in this
video clip.
- answer by Joe Yoon
- answer by Jeff Scott, 21 November 2004
Related Topics:
Read More Articles:


|
Aircraft | Design | Ask Us | Shop | Search |

|
|
| About Us | Contact Us | Copyright © 1997-2023 | |||
|
|
|||