Aerospaceweb.org | Ask Us - NACA 4-Digit Airfoil Equations

NACA 4-Digit Airfoil Equations

T(X)=10*TC[0.2969(X/C)^0.5-0.126(X/C)-0.3537(X/C)^2+0.2843(X/C)^3-0.1015(X/C)^4]

In addition, how were the parabolic equations used to calculate the mean camber line derived? Why do they have boundary conditions at x=0, x=p, and x=c?
- question from Yasser

The majority of this question was already addressed in a previous question we answered on the NACA airfoil series. In particular, we introduced the equations describing the thickness and camber lines of the Four-Digit Series. Refer to the link for a more detailed discussion of what a Four-Digit Series airfoil is and how to compute its coordidnates, but the three principal equations are repeated below for the sake of this answer. The thickness and camber of such airfoils are computed as follows:

Although the first equation is of a slightly different format than the T(X) equation that you are asking about, it will produce the same results as our y_t equation. Similarly, the two y_c equations are the parabolic equations you describe in your question.

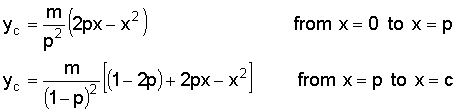
Those preliminaries aside, let's get down to the heart of your question--where do these equations come from? I think you have a false impression that these relationships were somehow derived from some fundamental concepts of mathematics and physics, but this is not the case. The thickness equation, for example, is actually based on empirical studies conducted by NACA back in the 1930s. Until that time, airfoil design was really little more than magic. Early aircraft designers had experimented with a number of diferent shapes and just happened to stumble across a few that worked very well. No one really understood why some shapes worked and others didn't, so there was no theory to guide designers in selecting the best airfoils for a given application. Picking the right shape was a matter of luck.

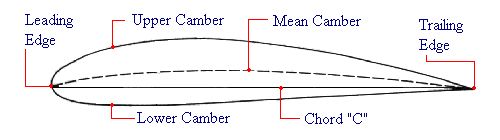
Researchers at NACA were very curious about this subject, and one of the first major efforts undertaken by the organization after its founding was to bring some logic and reason to airfoil design. They started by trying to understand why some airfoils worked well and others did not. In the process, they realized that there were a lot of common features shared by the airfoils that were most successful. These features could be reproduced by a simple combination of a mean camber line and a thickness distribution. As illustrated below, the mean camber line (or simply "mean line") is a line running along the center of the airfoil. It can be thought of as the average of the upper surface and lower surface of the airfoil shape. The thickness distribution defines how thick the airfoil is at any point along its length above and below that mean line.

Parts of an airfoil

Armed with this knowledge, the researchers defined some simple algebraic equations that could be used to generate a family of airfoils similar to the successful shapes from which the equations were derived. The equations they came up with are empirical relationships. In other words, they happen to mathematically produce shapes similar to existing airfoils, but there is no fundamental theory underlying their development. They are merely equations that happened to fit the existing airfoil coordinate data. The mean camber line equations, in particular, were simply chosen to be parabolic equations arbitrarily since an equation of that form just happened to match the camber lines used on many of the successful airfoils of the day. By changing the value of p and its x-position along the chord, parabolic equations matched up well with the camber lines for these existing shapes.

Since you asked about sources describing how these equations were developed, you can read more in two classic publications:

A research paper entitled The Characteristics of 78 Related Airfoil Sections from Tests in the Variable Density Wind Tunnel, NACA Report #460, by Jacobs, Ward, and Pinkerton, 1932. This paper is available on the NACA database at http://naca.larc.nasa.gov/reports/1933/naca-report-460/. See the pages labeled 300-301 for a discussion of the thickness and camber line equations.

A book entitled Theory of Wing Sections by Abbott and Von Doenhoff, 1959. This is a very popular book summarizing the basics of all the NACA airfoil series, and it should be easy to find in a technical library. In particular, Chapter 6 covers the airfoil coordinate equations.

The basic point to remember from all this is that the NACA 4-Digit airfoil series was not created using some advanced mathematical derivation. Researchers utilized a fairly simple algebraic approach to creating this series, but it had a revolutionary impact on aeronautics. The method provided designers and manufacturers with a powerful new tool in selecting airfoils for their vehicles and brought a sense of order to a field where there had been nothing but chaos before.
- answer by Jeff Scott, 27 October 2002

I am interested in defining the airfoils for the A-4 Skyhawk and S-3 Viking. The section designations are of the form NACA 0008-1.1-25 and 0016.3-1.03 32.7/1.00. I have read your previous explanations on modified four and five digit aifoils and still have a hard time defining it. Can you help me out?

I am doing my utmost to build a 100% scale radio-controlled flying model of the FB-111A. The airfoil sections listed for this aircraft are the NACA 64A210.68 and 64A209.80. Can you explain what these names mean and how to compute the airfoil coordinates?

Aircraft | Design | Ask Us | Shop | Search