Aerospaceweb.org | Ask Us - Finite and Infinite Wing

Finite and Infinite Wing

- question from Ken Rieder

You are partially correct. As you surmised, the difference between a finite wing and an infinite wing is in that a finite wing has tips. As a result, the higher pressure air from beneath the wing tries to move around the tips towards the lower pressure above the wing. This motion creates a swirling vortex of air from each tip that trails behind the wing. For that reason, we call these vortices trailing vortices. You can read more about this phenomenon in a previous question about ground effect.

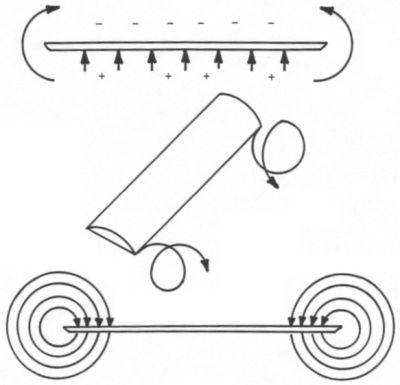
Creation of trailing vortices due to a difference in pressure above and below a lifting surface

However, you have the terms 2D and 3D reversed. A 2D wing is the same as an infinite wing while a 3D wing is a finite wing. We call a finite wing "3D" because the air is able to travel up and around the wingtip to produce trailing vortices. The flow around a 2D wing is not able to move in this third dimension. This situation is not possible on a real aircraft since one cannot build an infinite wing. However, an airfoil section tested in a wind tunnel is a 2D wing because the walls of the tunnel prevent the flow from being able to travel around the tips. An example of a 2D wing being tested in a wind tunnel is shown below. In this case, the wing is mounted vertically so that the floor and ceiling prevent the air from being able to flow around the tips.

2D infinite wing being tested in a wind tunnel

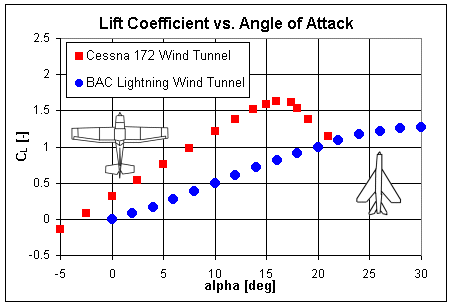
Aerodynamically, the effect of trailing vortices reduces the slope of the coefficient of lift vs. angle of attack curve. The lower the aspect ratio of the wing, the more the lift-curve slope is reduced. This behavior results from the fact that the trailing vortices are able to influence a larger portion of the wing the smaller the wingspan becomes. The ideal lift curve slope of any 2D wing is 2π. If you look at wind tunnel data for any airfoil shape, you'll see that the slope of the lift curve is indeed very close to this value. As aspect ratio decreases, however, the lift curve slope becomes less than 2π which reduces the overall lift that the wing can produce. You can learn more about this behavior in an article about estimating the lift coefficient.

The reasoning above explains why commercial airliners like the Boeing 747 and other long-range aircraft like the B-52 Stratofortress bomber have very long, slender wings. These wings have a high aspect ratio that reduces the effect of trailing vortices and maintains a high lift curve slope. Such a wing is more aerodynamically efficient and allows the plane to maximize its range.

Overhead view of a B-52 illustrating its high aspect ratio wing

By contrast, most fighters like the F-16 Fighting Falcon or MiG-21 have very short, stubby wings. These aircraft need to be very fast and maneuverable, which requires low aspect ratio wings. The drawback of this design is that such planes typically have a very short range.

MiG-21 fighter showing its low aspect ratio wing

You can see the effect of aspect ratio on the lift produced by a wing quite clearly in the following graph.

The data compares the lift coefficient of the Cessna 172, which has a high aspect ratio wing, against the lift coefficient of the Lightning, a supersonic fighter with a low aspect ratio wing. The slope of the Cessna 172 curve is clearly much higher than that of the Lightning up to the stall angle. At any angle of attack below stall, the Cessna will have a higher lift coefficient and be a more efficient wing.
- answer by Jeff Scott, 14 March 2004

I am involved in wind tunnel experiments working with different shapes. I'd like to know the drag coefficient for a cylinder and a cone with its point facing into the wind. Are there any simple approximations?

Aircraft | Design | Ask Us | Shop | Search