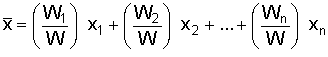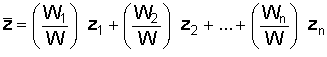Center of Gravity
How is the center of gravity of an airplane calculated?
- question from Akhilesh Kumar Kashyap
The center of gravity (CG) is the point about which the weight of an aircraft is equally distributed. If you were
to suspend the aircraft from this point, it would be perfectly balanced. The location of the CG is crucial for
such purposes as aircraft stability, control surface design, and landing gear design. If the CG is too far
forward, the control surfaces will be unable to trim the aircraft. If too far back, the plane becomes unstable.
The position of the CG changes throughout an airplane's flight as fuel is burned, bombs are dropped, landing gear
are extended and retracted, and so on. Thus, the aircraft designer must be very careful when placing each
component within the aircraft to maintain its stability and controllability throughout the range of operating
conditions and stages of flight.
The relationship used to compute an airplane's center of gravity (CG) is actually quite simple. What is often
difficult is estimating the weights of all the major components and where those weights act. In general, the CG is
computed by the following method:
- Select a baseline point from which all dimensions are measured, or a datum. We typically use the
airplane nose and measure all distances aft of this location.
- Estimate the weights of the major components (engines, fuselage structure, tail assembly, landing
gear, wing structure, control surfaces, fuel load, pilots, passengers, payload, avionics, etc.)
as accurately as possible. In the early stages of design, we may only be able to make rough
guesses, but our estimates become more accurate as specific systems and materials are selected.
- Estimate the center of gravity of each component and measure its location aft of the datum point.
Again, we may be forced to use rough approximations until the design becomes more settled.
- Sum up all of the component weights to determine the total weight of the airplane.
- Compute the CG of the entire aircraft using weight ratios (i.e. weight of the component over the total
weight) and summing up the moments created by each component about the datum point. The position
of the CG along the length of the aircraft is computed by the following equation, where
Wn/W is the weight of each component divided by the total weight and xn is
the estimated CG of that component.
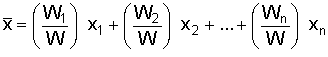
- The above equation gives us the x-location of the aircraft CG. If we want to know the z-location, we
follow the same procedure. We need to select a new datum point, typically the ground, and measure
the centers of gravity of each component from this location. We can then compute the height of
the CG by this equation:
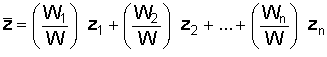
- Assuming that the aircraft is symmetrical, the y-location of the CG should be the centerline of the
aircraft (or y=0). However, there are a few asymmetrical planes out there, and the CG calculation
can be performed using the same method previously discussed.
An example of this procedure is illustrated below:
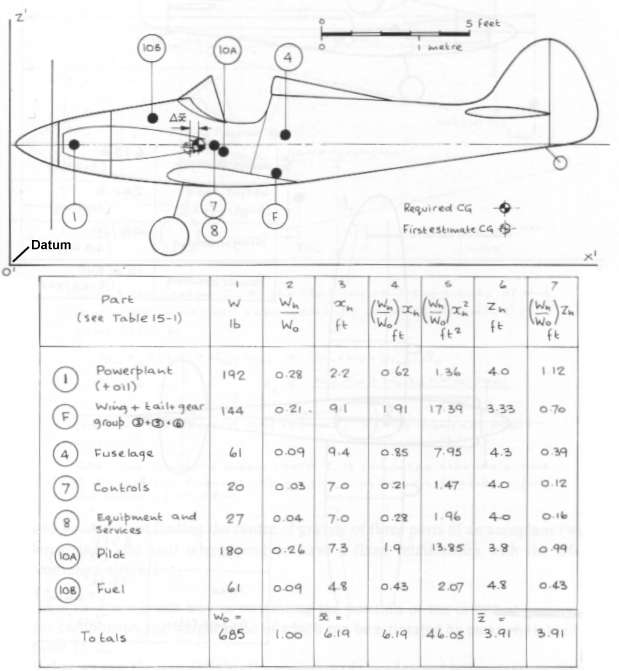
Computing the CG of an airplane
Methods of estimating the weights and locations of each of these components can be found in any good aircraft
design textbook, such as
Design of the
Aeroplane by Darrol Stinton or
Aircraft Design: A
Conceptual Approach by Daniel Raymer.
To see an example of a real-life application of determining the center of gravity, check out the
Weight and Balance section of the
Storm Shadow UCAV design project. Note that the CG is calculated for
a number of conditions (aircraft empty, fully loaded, landing with and without payload, etc.) corresponding to
different phases of the plane's operation.
- answer by Joe Yoon, 22 July 2001
Read More Articles: